Part I: Background, Premise, and Setup
Inherent in the desire to develop better baseball statistics–and as a result, improve baseball analysis–is the belief that this information is not only available but also not being used by the men and women who run baseball. As Moneyball and the resulting reaction has showed, some General Managers seem to be using the same methods for performance evaluation that were used 20 or 40 years ago.
It therefore stands to reason that GMs are paying players not for actual performance, but rather for perceived performance as viewed through the rusty glasses of decades-old beliefs about the statistics of the game. For this study we wanted to find out if General Managers were, in fact, paying players along the lines of their objective “value” (as defined by VORP), or if there was something else in play.
One of the biggest challenges for the study was finding a proper data set. It seems clear that the best set of players to use was free agents. These players have their salaries determined on what is (arguably, for sure) a decent approximation for a free market, or at least the closest MLB is going to see. As economic theory tells us, these players will then be signed for something approximating their true value.
To provide a brief example, let’s pretend slugging first baseman Joe Schmoe is a free agent. If he is perceived to be worth $10 million, then if the Knights and Bears are in the market for a first baseman and have the money, it is clear that both will be willing to spend up to $10 million. Anything over that and Mr. Schmoe will not be worth the money, so his suitors will pass. Thus, Joe gets his $10 million, and more or less, whichever team offered it first gets the first baseman.
This model relies on three key assumptions. First, there are at least two teams interested in each player. This assumption is not much of a problem, since it seems unlikely that a particular player will only fill one team’s needs. Second, the teams interested in a player are willing to spend as much as he is worth. As stingy as some teams might be, it again seems unlikely there will only be one team willing to spend as much as a player is perceived to be worth. Finally, we assume that a player has a single specified value. This assumption is a little shakier since a team with two solid first basemen is unlikely to be willing to spend much on Mr. Schmoe; but it does seem plausible that the few teams in the market for a slugging first baseman would place similar values on a particular player.
We decided it would be best to use players who were free agents before the 2003 season. It seems likely that the Collective Bargaining Agreement (CBA) that MLB was operating under would affect player’s salaries, so we wanted to use data from a single CBA. The most recent CBA was not completely resolved until some time after the 2001 season finished, so we felt it would not be appropriate to include players who were free agents before the 2002 season, due to the uncertainty surrounding the CBA under which some of the players might have been signed. We obtained data on free agents before the 2003 season and their salaries from the late (and quite great) Doug Pappas’ Web site.
The final decision concerning the data set was to determine which year’s statistics to use. We decided to use the players’ statistics from 2003. It stands to reason that when a GM signs a free agent, he is paying that player for future performance, not past. Obviously, the player’s performance in past seasons will play a large role in the GM’s decision, but his job, ultimately, is to determine how a player will perform in seasons for which he is under contract.
Part II: Data Compilation and Analysis
Having already established the choice of VORP as our measurement of a player’s true value and the 2003 salary as the GM’s estimation of the player’s value, we had to determine how to measure a player hitting for power. For our purposes, we considered several candidates as plausible measures of a player’s valuable contribution from power, including extra bases (XB=TB-H), total bases (TB), and home runs (HR). We also considered a few variants of summing the bases garnered from extra-base hits, like XB-3B, which works under the assumption that a triple is a double hit by a player with speed; so we should only consider the power aspect, and count a triple like a double.
Ultimately, we wanted to set up a bivariate regression trying to predict a player’s salary using his true value, for our purposes VORP, and the value he contributes in the form of power, with one of the measures mentioned earlier. After establishing a regression with a reasonable amount of explanatory power, we wanted to see exactly how much explanatory power each metric had. If the coefficient on VORP was not significant, and the coefficient on the power metric was significant (as we expected) then our results would show that GMs are overvaluing power.
To start the number crunching, we set up preliminary analysis that determines how high the correlation coefficient (r-squared) would be, using the varying possibilities for power metrics in a bivariate regression with VORP. This initial analysis suggested that using total bases would maximize the overall predictive power of the regression (see Charts 1 and 2). After selecting a suitable power metric, total bases, and setting up the bivariate regression, we had yet to run the regression and see which metric had more explanatory power.
Chart 1: Correlation coefficients for univariate regressions with selected power metrics predicting log(Salary)
Power Metric Model Correlation TB 0.4361 XB 0.4133 HR 0.3531 SLG 0.1721
Chart 2: Correlation coefficients for bivariate regressions with selected power metrics and VORP predicting log(Salary)
Power Metric Model Correlation TB 0.4402 XB 0.4226 HR 0.3966 SLG 0.3581
To correct for the exponential growth in salary data, we used the base 10 logarithm of salary instead (denoted log(Salary) from here on). These data are close to being linear, which means that fitting a linear bivariate regression is appropriate. Thus, we used VORP and TB to explain variation in log(Salary) by calculating a bivariate regression of the form:
After running the regression, the results were extremely encouraging. For the sake of being thorough, we also ran univariate regressions with both VORP and TB, then ran the bivariate combination.
There are two critical components of each regression. The first one is the overall explanatory power of the model itself, the correlation coefficient, referred to as r-squared. The second is a measure of the explanatory power of each independent variable. To measure the explanatory power of each independent factor, we wanted to see whether the estimate for the parameters on each of the independent variables and the intercept (here, the estimates for each ?) has a statistically significant variation from zero, called the t-value.
In each of the three regression models–the two univariate regressions and the single bivariate regression–we looked at the correlation coefficient for the entire model and the t-value probability for each parameter estimate (see Chart 3). First, compare the first two regressions, both univariate. The correlation coefficient for the model using total bases is much higher relative to the model using VORP. Both models indicate that the single regression parameter has statistically significant deviation from zero. The univariate model using total bases had a higher correlation than the univariate model using VORP. This hints at the plausible conclusion that total bases have more explanatory power than VORP when estimating a player’s salary.
Chart 3: Correlation coefficients and t-value probabilities for univariate and bivariate regressions with VORP, total bases, and both
Dependent Independent Correlation TB t-value VORP t-value Variable Variable(s) Coefficent probability probability log(Salary) VORP 0.3540 < 0.0001 log(Salary) TB 0.4361 < 0.0001 log(Salary) VORP, TB 0.4402 0.0061 0.5352
In the bivariate regression, the overall correlation is minimally greater than the univariate model using only total bases. This indicates that adding VORP to the regression gives very little additional information about the logarithm of a player's salary. That is, adding VORP into the regression that used only total bases only gave a very small increase in explanatory power for the overall model. Further, we found that the t-value probability was very large for VORP in the bivariate model. That means that there is a high likelihood that the parameter for VORP in the bivariate model is actually zero.
The t-value significance probability for VORP in the bivariate regression is 0.5352. This means that the probability that the parameter for VORP in the bivariate regression deviates significantly from zero is quite low. Thus, the addition of VORP to the model yields little additional information, at the cost of increasing inaccuracy.
As previously stated, these results provide strong evidence to our theory that General Managers are paying for power, not ability. To cover all our bases, we used the same process, substituting various measures of power (as mentioned above) for total bases. All of them yielded results similar to what we achieved here, save for SLG, which resulted in the estimate for the regression coefficient of VORP having a statistically significant difference from 0 (see Chart 4).
Chart 4: Results for bivariate regressions with selected power metrics and VORP predicting log(Salary), with correlation coefficient, t-value probabilities and actual parameter estimates
Power Model t Probability Regression Coefficients Metric Correlation Intercept VORP Power Metric Intercept VORP Power Metric TB 0.4402 0.0001 0.5352 0.0061 5.70182 0.00268 0.00300 SLG 0.3581 0.0001 0.0003 0.5616 6.03731 0.01479 -0.39738 XB 0.4226 0.0001 0.3608 0.0152 5.78397 0.00397 0.00565 HR 0.3966 0.0001 0.0558 0.0585 5.84591 0.00739 0.01562
Using these results, we can say that this data set indicates that hitting for power has a dominant effect in estimating the logarithm of a player's salary over the player's true value. Extrapolating these results into something a little bit more useful, we can say that it is apparent that General Managers give more weight to a player's ability to hit for power than his true value when determining his salary. This goes further to support the notion that hitting for power is attractive to GMs, and the theory that many GMs do not have a firm grip on a player's true value, at least in our estimation.
Part III: Future Considerations
In future work, we should look to analyze different types and sources of data to either support or refute these findings, as well as explore different facets of these theories. The first step in extending this study is to gather more data under similar principles: find players who signed a free agent contract, under the same Collective Bargaining Agreement, and compare their data in a similar fashion. We should also look to models using different measurements of power, other than those listed here. In addition, we might not decide to first maximize correlation coefficient, but instead find those models that have a statistically significant contribution from VORP, and subsequently try to maximize the correlation coefficient within those models.
There is also a tangential extension to this study that would serve to expand our general knowledge behind salaries. This particular model is actually quite poor. Concerning an attempt to actually estimate the player's salary (or the logarithm of a player's salary), there are several improvements that could be made, and two indicators are detailed below.
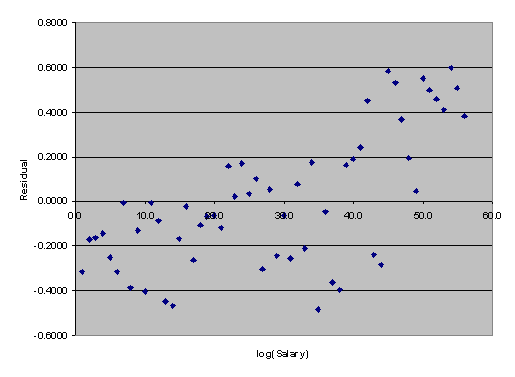
The first problem with this model is apparent in a visual representation of the residuals (see Graph 1). The linear trend in these residuals is quite noticeable. This trend indicates a structural problem with our model; if we were primarily concerned with the model's accuracy, we should rework the general format and setup of the model itself.
The second problem with this model is somewhat less apparent, and shows up when log(Salary) is plotted with the model estimate for log(Salary) (see graphs 2a and 2b in the appendix).
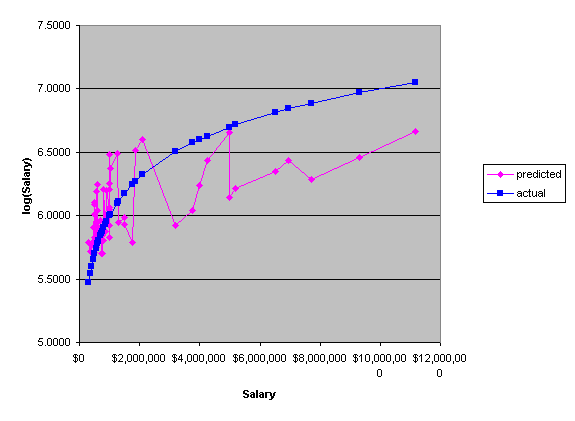
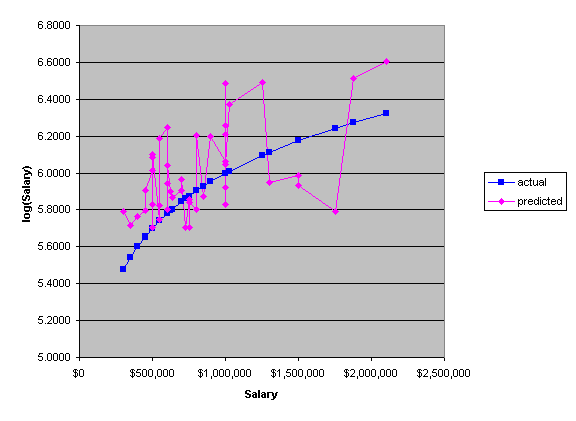
We can see that the actual log(Salary), the blue dotted line, is much more linear than the estimation of log(Salary). This wild fluctuation is due mostly to the fluctuation in VORP (see Graphs 3a and 3b).
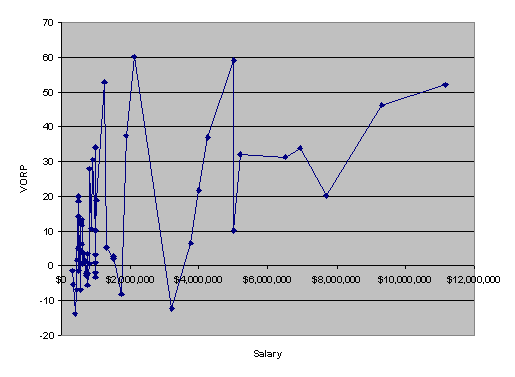
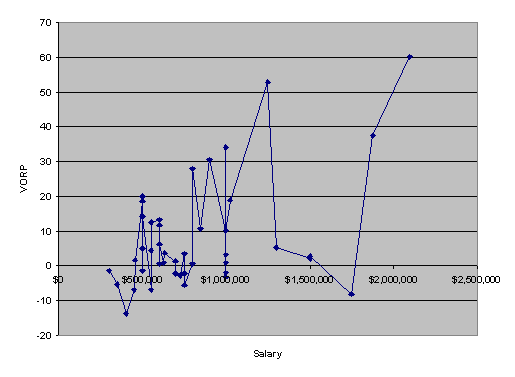
There is also a great deal of oscillation in the data for total bases (see Graphs 4a and 4b).
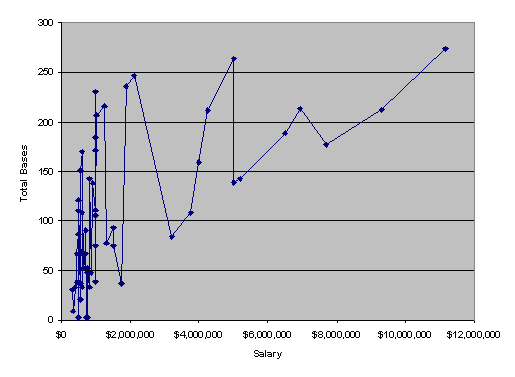
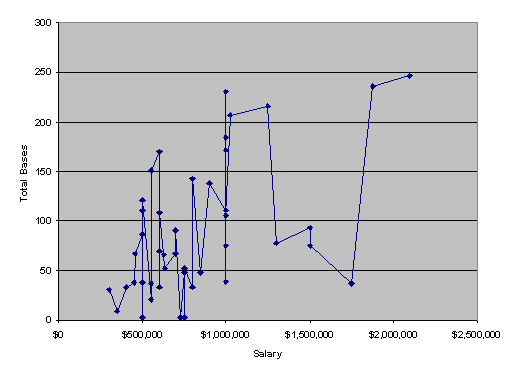
Note that in these graphs, the data are sorted by actual salary from least to greatest. Then, each the log(Salary), predicted log(Salary), VORP, and total bases are plotted in order. The oscillations in VORP and total bases have a significant affect on the oscillations in the predicted values, as you can see many similar patterns in these graphs. There is also reason to believe that there is a relationship between total bases and VORP that plausibly diminishes the value of having both in the regression, since adding duplicate data will often increase the variance of the estimate. With such linear data for log(Salary), it would seem that we should be able to find a suitable linear model to mimic the behavior of the data.
One of the more favorable solutions to this problem involves gathering more data, so that there is slightly less fluctuation in VORP and total bases. We might also bracket off the salary values into ranges, and consider each range separately, in addition to considering all the data as a whole. We could alternatively bracket the salaries and then average the data for VORP and total bases, so that we had a moving average, of sorts, for our independent data. Any time you start with such wildly oscillating independent variables, you are going to end up with an oscillating estimate.
With all of these concessions we should confess that the model was chosen initially to analyze the question at hand, and if we disregard that question, there is no reason to give an advantage to VORP or total bases in setting up a model to estimate a player's salary. The best strategy to creating a model to effectively estimate a player's salary is probably starting over completely.
Part IV: Conclusions
Our results provide strong evidence that GMs are, in fact, paying more money for power than that power is contributing to the team's performance. Regressing log(2003 salary) on 2003 VORP and total bases for players who were free agents before the 2003 season, we found that VORP was not statistically significant from 0--that is to say, players with similar total bases but very different VORP totals received similar salaries in the sample. This result suggests that despite continued advancements in baseball analysis, GMs continue to pay more money for power hitting. While it is outside the scope of this study to measure whether additional home runs or wins attracts more fans to the ballpark, we can conclude that by shifting the emphasis from power to performance, many general managers could be getting more wins for their buck.
Ben Murphy is a Baseball Prospectus programming intern and student at the University of North Carolina, Chapel Hill, majoring in Mathematical Decision Sciences. You can e-mail Ben at bmurphy@baseballprospectus.com.
Jared Weiss is a student at the University of Chicago majoring in Economics. You can reach Jared at jared@uchicago.edu.
Thank you for reading
This is a free article. If you enjoyed it, consider subscribing to Baseball Prospectus. Subscriptions support ongoing public baseball research and analysis in an increasingly proprietary environment.
Subscribe now