We heard the first blows in the nascent MVP debate of 2014 unfold just last week. At the time, Alex Gordon led all players in fWAR (by a narrow margin), largely on the basis of his extraordinary defense in left field (15 fielding runs above average, fifth highest in MLB). In response, Jeff Passan wrote that the idea of Alex Gordon as the best player in baseball was absurd.
Much wailing and gnashing of teeth ensued. To some of the doubters of sabermetrics, Gordon’s triumph on the leaderboards was yet more proof of the uselessness of WAR(P). To others, arguments against Gordon may have seemed ill-formed.
Fortunately, Gordon no longer leads baseball players in any of the flavors of WAR(P) (whew, argument defused). Even so, Alex Gordon brought to the surface a recurring theme in criticisms of the WAR framework: the weighting of defensive metrics. In theory, a run saved is a run scored. But whereas the relationship between singles, doubles (etc.), and runs produced is easily parsed with linear weights, defense is more difficult to measure. The steps between the events on the field and the runs being saved require more estimation, and that potentially injects more error in the final result.
A natural response to the additional error implicit in defensive measurements is to deem them unreliable and regress them according. ‘Regression’ exists in the sabermetric lexicon as both an abstract concept and a concrete, mathematical transformation. In the abstract sense of the word, to regress a player’s defensive WAR(P), for example, is to mentally adjust his contribution back toward the mean, accounting for the uncertainty in the estimate—exactly what we’d like to do with defense. We can formalize that mathematically by simply multiplying each player’s defensive value, calculated hereabouts as FRAA, by some constant which I’ll call a “regression factor,” r:
FRAAi x r = regressed FRAA of player i
When r is less than one, a player’s defensive contribution is being pushed back towards zero, which is to say the average. For example, at a regression factor of .5, a defensive standout like last year’s Manny Machado loses half of his value, i.e. about 14 runs. Meanwhile, a defensively mediocre player that year, Matt Carpenter, also sheds half of his value, but this only amounts to a single run subtracted. The penalty is thus much stiffer at the extremes, both good and bad. Consider the following graph, which shows the density of players at different FRAA values, with and without a regression factor of .5 applied.
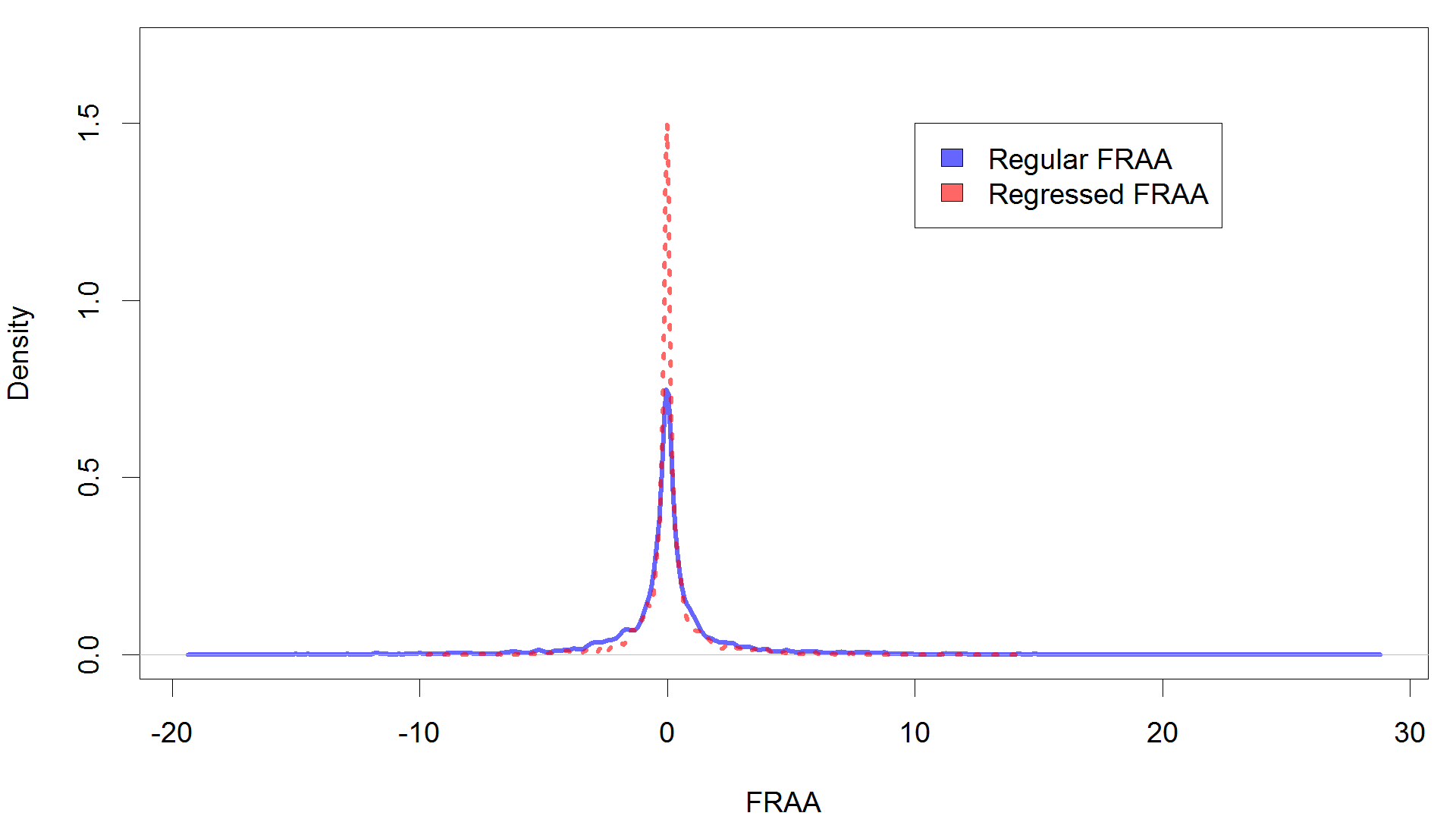
You can see that applying a regression factor less than one effectively compresses the distribution of defensive talent in MLB.
When r is greater than one, conversely, you are accentuating the defensive differences between players. Suddenly, Machado’s defense goes from merely outstanding to more valuable than Adam Jones’ offense in 2013. This change corresponds to a very anti-Passan idea: defense is actually undervalued.
Suppose that we do decide to regress defense somehow. The question becomes then how much regression to apply. At one extreme, a regression factor of 0 effectively discards defensive metrics altogether. At the other, we could over-emphasize them to the point of ridiculousness.
Fortunately, we can use past data to guide our search for the optimal regression factor. The idea goes like this: pitching statistics, say ERA, are the result of some combination of 1) the skills of the pitcher, 2) the skills of the defenders behind him, and 3) luck. We can’t do anything about 3), but we can change the relative weights we assign to the pitcher and his defenders. If, when we regress out the summed contributions of defenders, we are better able to predict the resulting team’s ERA, then this would be evidence that we need to downweight defense to a greater degree.
I’ll look at this at the team level, using the past three years as my dataset (2011-2013). I first looked at the fit of the model when we use the default, that is, a run scored is a run saved. Then, I varied the regression factor, both higher and lower than the default (r = 1). I scored the fit of the model to ERA by looking at the root-mean-square error (RMSE); when this value is high, the model fit is poor, and when low, the model fits the data better.

For FRAA, we see that downweighting defense via the use of a regression factor less than one results in a worse fit to the model. At the extreme of r=0 (disregarding the defensive stats entirely), the model fits the least well (RMSE>.4). To put it another way, defensive stats may be unreliable, but they are measuring something, and when we take them into account, we are better able to predict and understand the results on the field.
Somewhat surprisingly, the model best fits the data (RMSE is minimal) when FRAA is overemphasized, to the tune of r ~ 4. There is some sense to underweighting defensive statistics, given their unreliability, and I would note that the difference throughout the whole range of regression factors is small.
It’s not WARP that prompted the debate, however. It all started with the FanGraphs dWAR, and we can take the very same approach to that slightly different variety of WAR. To recap, I’ll vary the regression factor across some range, checking a linear model’s fit to ERA at each step to determine the optimal regression to apply to our defensive metrics.

Just as with BP’s FRAA, the UZR-based dWAR of FanGraphs contributes some accuracy to our model of ERA. And, as with BP’s defensive metric, if any error is being committed, it’s that we are not weighting defense enough. For optimal accuracy, we should be accentuating the differences between players’ defensive statistics, not regressing them.
These results shouldn’t be entirely surprising. Defensive WAR is not a truth revealed from on high; it was designed (by very capable sabermetricians) with full knowledge of the fact that it improved our understanding of runs allowed. The coefficients which translate defensive play into runs weren’t chosen arbitrarily from a hat or a random number generator, but rather calibrated with at least some attention given to the resulting models’ ability to fit things like ERA. For this reason, we shouldn’t be surprised to find that our defensive metrics are well-suited to predicting ERA. Indeed, I would bet that the small error observed in both models (FG and BP), in which defensive metrics are perhaps slightly underutilized, is by design.
Considering this experiment, I don’t think that there exists any particular issue with the weighting of defensive WAR as a whole, despite Passan’s argument. There might be a problem with Alex Gordon’s dWAR in particular (or Adeiny Hechavarria’s, or whoever’s). Yet, the overall weighting of dWAR is reasonably accurate, or it would have been discarded for something different.
I’ve approached this issue of defensive metrics using a Large-N framework, that is, evaluating our models on the basis of the behavior of a lot of players over a sizable stretch of time. However, I suspect that the problem is with particular players, and the notion that individual defenders are worth as many wins above replacement as the models suppose. That small-N (or even N=1) problem is a much more difficult one to engage with or disprove.
The good news is that whatever your stand on defensive metrics, the problems inherent in them may soon disappear. With the impending arrival of Statcast, we will be able to root our defensive metrics in numbers every bit as solid as singles, doubles, and home runs. We’ll be able to decompose a given player’s contribution to individual plays, as well as individual skills. Alex Gordon’s defensive brilliance will become a combination of Alex Gordon’s incredible reflexes, measured as reaction times, combined with his astounding speed, measured as miles per hour of outfield grass covered, and coupled to his fantastic arm.
Defense will still be complex, mind you. There are problems of positioning, and coaching (the rise of the shift), and the ways in which multiple defenders can play a role on the same play. But with luck and some Gory Math, all of those difficulties should yield, and we ought to end up with a better framework for dWAR when all is said and done. In the meantime, defensive metrics are at worst being over-regressed, perhaps in accordance with our uncertainty about them.
Thank you for reading
This is a free article. If you enjoyed it, consider subscribing to Baseball Prospectus. Subscriptions support ongoing public baseball research and analysis in an increasingly proprietary environment.
Subscribe now
2. Shouldn't the regression factor be individualized for each player? For example, it makes sense to me that rookies should have a very large regression factor towards the league mean - or the historical league mean for rookies - which might be more generous than the league mean, because players lose range as they age. We don't know if a rookie's defense is reliably as good as the runs he has saved so far in the season. However, the later in the season, the less we need to regress the rookie as he has a larger sample size to establish a defensive ability. Instead of regressing towards a league mean, a veteran should be regressed towards his own normal defensive prowess - with an aging factor to it - as we do with batting projections.
3. Come to think of it, this is how we should consider players when voting for all-star teams, post season awards, or single season fantasy teams: something that is a mix of what they've done - both offensively and defensively - and what we would project from them - in order to get the most accurate view of how good they really are.
Unless you think that measurement uncertainty varies by player (which is entirely possible, but beyond the scope of this article), it would not be appropriate to apply a different regression factor to each player. You would apply a different factor when trying to estimate true talent levels, since they clearly do differ by player, but as I mentioned, that is a slightly different problem.
However, I don't see a big difference between how we measure hitters beyond the three true outcomes and using zone factors that cover the whole field for fielders.There is probably just as much luck involved. If anything there is more subjectivity in what is a hit as it could be judged as an error. A regression factor is therefor equally applicable.
(team ERA in year i) ~ ((pitcher WAR(P) in year i) + (defensive WAR(P) in year i))
Am I right in thinking that FRAA is regressed at the level of each individual player? If so, does that mean that at the team level it would be over-regressed because the team sample is much bigger than each individual sample? That might explain why you need to 'unregress' FRAA to get the most accurate model.
That said, am I remembering correctly that dWAR and UZR already include the effect of errors? If so, we'd seem to be introducing an incongruity by relating these metrics to ERA rather than to RA.
I'd expect minimal impact, if any. Just seemed weird. Thanks again for the work.
The only reason was a practical one: I couldn't figure out an easy way to calculate dWAR(P) without taking errors into account, so I just left them in. If anything, it would push the model to be less accurate (greater RMSE).