On Friday, Bill Petti wrote an interesting article at the Hardball Times on predicting the success of hitters based on the way pitchers attack them. If that sounds familiar to you, dear reader, it might be because it’s a topic about which I have written at great length in the recent past. To recap, I found that changes in the distance at which a pitcher threw to a batter could predict whether a batter was primed for a breakout or, conversely, likely to underperform his projection.
Petti found very different results in his study, however. Using a metric of his own invention called Heart%, Bill found that there was no trace of predictive power in changes in Heart% both within and across years, replicating the general approach which I had used. Let me say at the outset that I have the greatest respect for Bill and his work, especially with regards to the zone partitioning scheme which he and Jeff Zimmerman invented (which resulted in the useful statistic Edge%). So I do not mean the remainder of this post to denigrate in any way the work Bill did in this or other studies.
With that said, it’s unsettling when other analysts fail to replicate one’s results. I set out then to examine why Bill’s study didn’t reproduce my findings, and what, if anything, it can teach us about predicting batter breakouts and the strike zone in general.
It’s important to note that Bill used a different metric than I had examined. Heart% is based on dividing the strike zone into five different areas. Four of these areas are edges (up and down, left and right). The fifth is the heart, the definition of which I take from his article at THT dated May 5th, 2014:
RHH: (px >= -.43 and px <= .7) and (pz >= (1.22 + Batter Height/12 *.136) and pz <= (2.30 + Batter Height/12 *.136))
LHH: (px >= -.9 and px <= .21) and (pz >= (.65 + Batter Height/12 *.229) and pz <= (1.7 + Batter Height/12 *.229))
In my researches, I have used a slightly different methodology. Instead of dividing the zone into regions, I’ve considered a simpler measure, which is simply the average distance between the locations of all pitches and the center of each batter’s strike zone. I call this measure zone distance.
Let’s pause for a minute and consider how these metrics differ. Heart% is based on dividing each pitch into one of two categories: in the heart of the zone or out of it. It is therefore based upon binary data. Zone distance is a little richer than that: pitches can be near or they can be far or they can be anywhere in between. Heart% implicitly treats all pitches outside of the heart the same, and all pitches inside of the heart the same; zone distance allows every pitch to vary.
I think this fact is important, not least because baseball is a game of inches. I’ve shown before that tiny differences in pitch trajectory separate groundballs from flyballs, and singles from home runs. Not all pitches inside or outside of the zone’s heart will be equally hittable: the further away, in fact, the less hittable it will be.
Still, Heart% is fundamentally measuring something similar to zone distance. So there ought to be some relationship between a batter’s skill level and his Heart%. In fact there is a decent relationship:
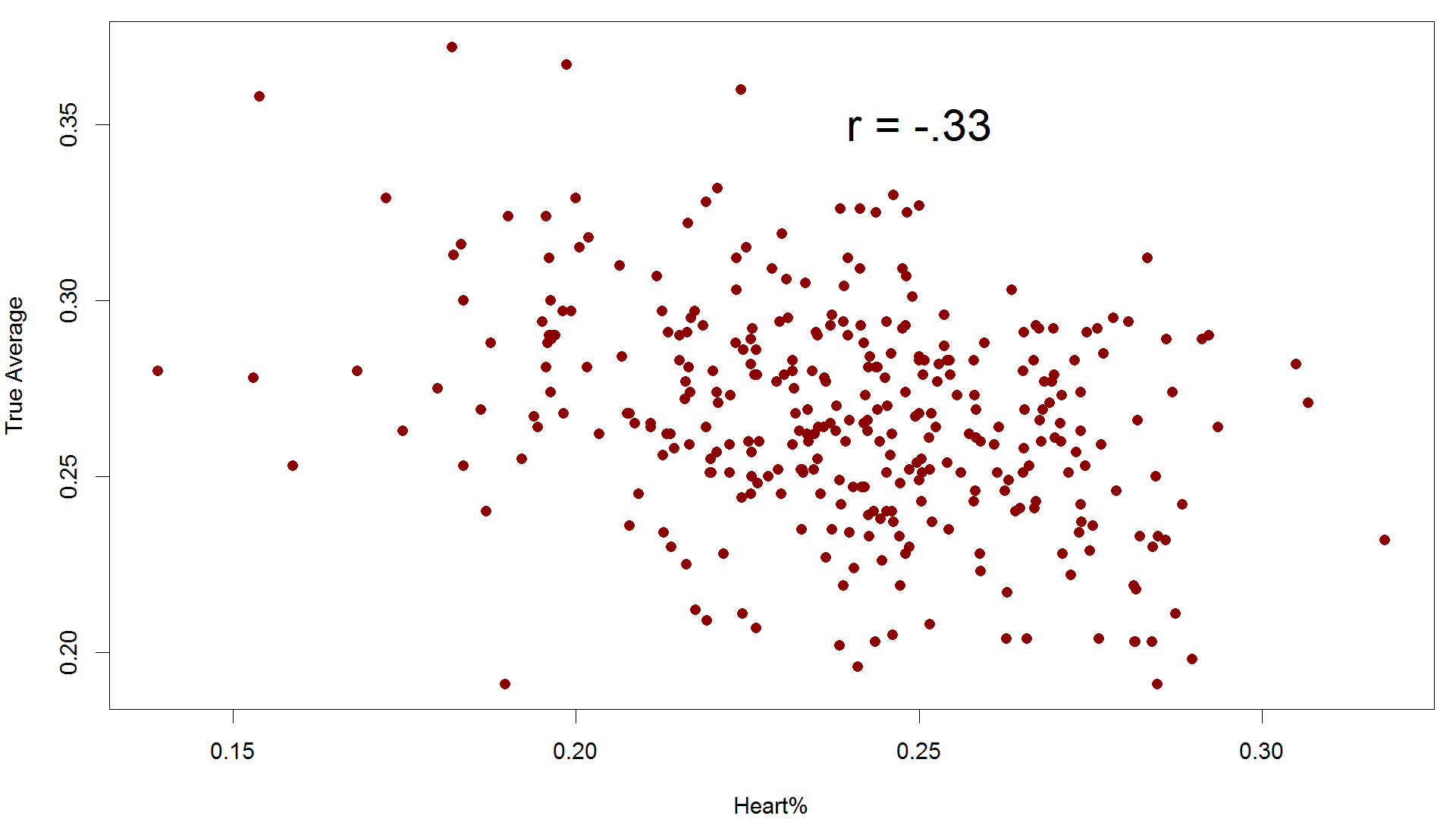
The R2 between Heart% and TAv is ~.1, so we say that Heart% explains 10 percent of the variation in True Average. More to the point, it’s not as strong as the relationship between zone distance and TAv.
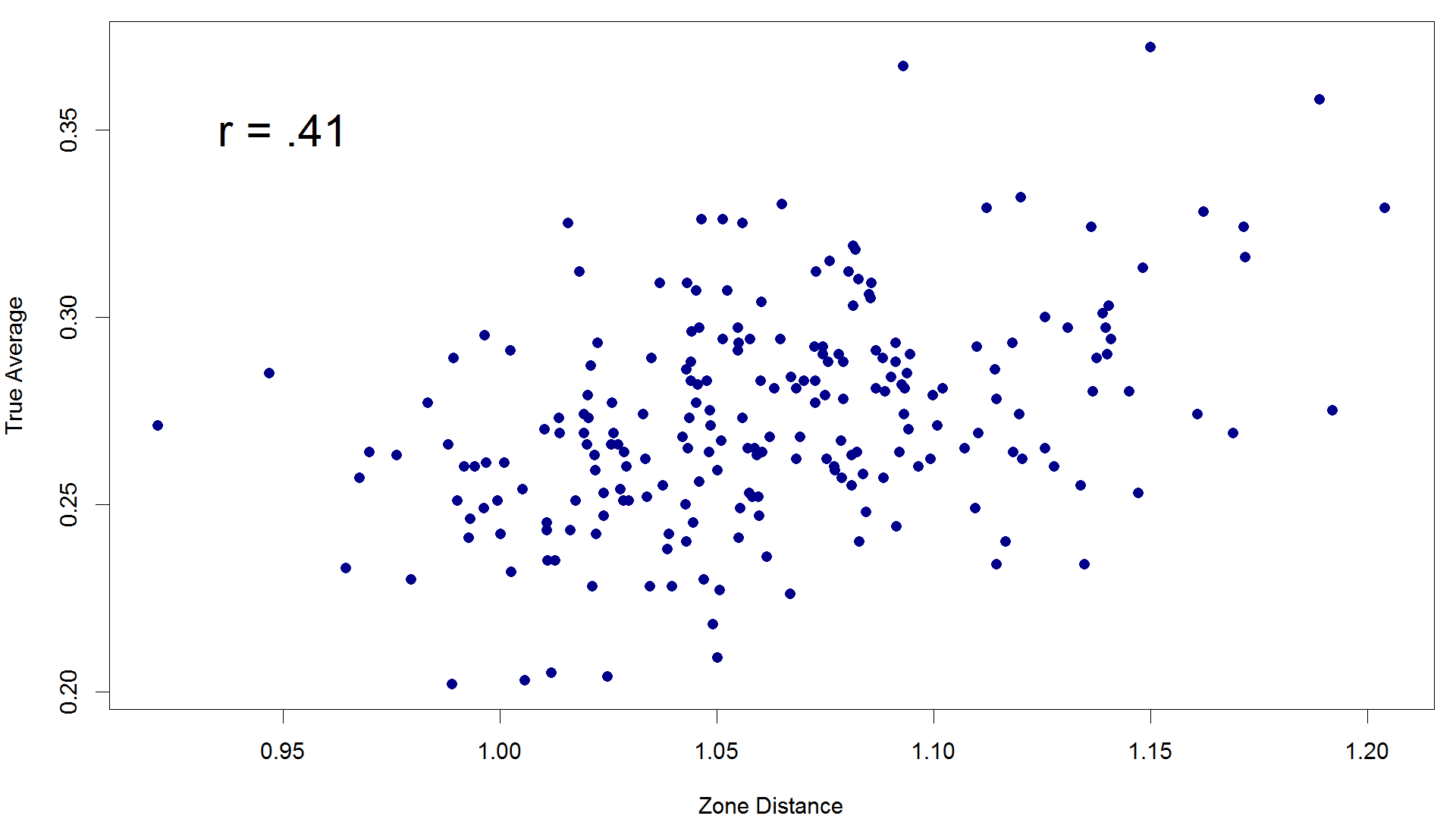
Because R2 is, well, squared, it accentuates the difference between Heart% and zone distance. Zone distance explains 16 percent of the variation in TAv. Note that I am performing this comparison at a relatively low number of pitches (1,000): as you increase the number of pitches cutoff, the difference between correlation coefficients narrows, suggesting that Heart% requires more data to stabilize. There is no cutoff I could find for which Heart%’s correlation overtakes zone distance’s, however.
All things being equal, I think Heart% is a little less connected to a pitcher’s evaluation of a hitter’s skill level than zone distance*. If we are now using these two statistics to parse changes in pitcher opinions of batter skill levels, the metric which is better correlated with pitcher opinions to begin with will be better suited to the task.
In his article, Bill did a very thorough job of showing that change in Heart% did not, in fact, improve Marcel-based projections of player performance. I won’t reproduce that work here (you should go read the article for details), but I did want to apply his method to zone distance in order to show that it does indeed function as a breakout predictor.
The method I’ll implement is to look at the year-on-year difference in TAv by fitting a linear model consisting of 1) PECOTA’s preseason projection and 2) the trend in zone distance over the course of the full season (excluding playoffs). I use the three-year** stretch 2012-2014, and consider all batters with more than 1,000 pitches.

Both PECOTA’s projections and the zone distance trend contribute statistically significant explanatory power to the regression. Obviously, PECOTA does most of the work: PECOTA alone results in an R2 value of .273***. But that’s not to say that zone distance doesn’t contribute something: it adds a large boost in accuracy, but only to a handful of players like Chris Davis who significantly defy their projections. Consequently, if I remove players whose performance differs from their projections by more than .050 points of TAv (in either direction), the significance of zone distance is drastically reduced (the p-value goes to .09). For the remainder of the players, zone distance is largely irrelevant. This contrast is the reason I initially used the top and bottom 10 to make my breakout and breakdown predictions, and it highlights the need for more complex, potentially nonlinear models to take zone distance trends into account properly.
Checking Up on the Predictions
I didn’t just say that zone distance changes predicted breakouts. I put my money where my mouth is by providing a list of 12 players who, by the method I had initially used, were in line for significant overperformance of their PECOTA projections this year. At that time, the season was only a few dozen games old, so the TAv marks players had were still fluctuating wildly (hey, remember when Charlie Blackmon was on pace to be MVP?), and these were truly predictions: I based them solely on 2013’s zone distance trends. So as a gut check on the accuracy of my results, we can look at how they are doing so far.

As it turns out, they are doing quite well. There are some exceptions, and of course the dreaded Ibanez drags the whole population down, but on average, this group is overperforming its PECOTA projection by .09 points of True Average, which is to say nearly exactly the same margin as the previous year’s breakout candidates. The median, instead of average, performance is even better at +.021 above PECOTA.
Now let’s say that I hadn’t truly identified any particularly special group of players, and had instead sampled a dozen hitters at random. What are the chances that I would have picked a group of 12 players who outdid their PECOTA projections by a median of +.021 points? One can estimate that via repeated random sampling, and it turns out that the chance is low, about .03, suggesting that the breakout prediction method I used actually works.
From this group, the player whose prediction I am most proud of is Victor Martinez. Nobody saw Martinez’ breakout coming, and whole articles have been written about the improbability of VMart’s resurgence. My method would—and did—predict it, and although he’s probably not likely to continue beating his projections quite as severely as he has so far, I would bet that he ends the season solidly overcoming even the most optimistic projection (the 90th percentile of his PECOTA projection entailed a TAv of .290).
Conclusions
The metric of Heart%, while correlated with zone distance, shows a slightly weaker relationship with hitting skill than zone distance does. I suspect that the difference in results between Bill’s study and my own may stem in part from that slightly weaker correlation between the metric of interest and a hitter’s skill. Using Bill’s general method, I do find that zone distance adds to PECOTA’s level of predictive accuracy, but only marginally, and for certain hitters. Even so, a simple threshold-based metric was able to correctly identify a pool of hitters who are collectively outperforming their predictions by a statistically significant margin, which holds promise for improving projections in the future.
*I made bootstrap confidence intervals on the correlation coefficient. About 6% of the bootstrapped correlation coefficients were less than <.33 (the correlation coefficient of Heart% and TAv), so there is a not quite (p ~ .06) statistically significant difference in correlation coefficients.
**I used three years because that was all the PECOTA projections I had handy. There is no reason to believe results would be different in five years instead, however.
***This R2 value is lower than what Bill cites as Marcel’s accuracy in his article. Don’t be fooled however: PECOTA is more accurate than Marcel in exactly matched circumstances. Because I am imposing a less severe PA cutoff, I am allowing PECOTA to predict players for whom there is less data available, hence the prediction is less accurate in comparison to when Marcel predicts players with more PAs.
Thank you for reading
This is a free article. If you enjoyed it, consider subscribing to Baseball Prospectus. Subscriptions support ongoing public baseball research and analysis in an increasingly proprietary environment.
Subscribe now
By the way, minor note: I am using the actual distances from the center of the zone (based on the Pitchf/x px and pz coordinates) rather than the more commonly used Zone% statistic that shows up in, e.g., BP's Plate Discipline section.