The following article, written by Keith Woolner with Rany Jazayerli, appeared in Baseball Prospectus 2001.
Table of Contents
- Long-term injury risk
- Pitch counts and injuries
- Data to be studied
- Identifying Injured Pitchers
- Defining Comparable Pitchers
- Career PAP as a Predictor of Injury
- The Workload Stress Metric
- The Injury Likelihood Equation
- Statistical Significance of Results
- Other PAP formulae
- 2000 Workload Stress leaders
- Conclusions and Futures
- Acknowledgements
In the previous article, we derived a new PAP formula (dubbed PAP^3) that reflects the typical short-term decline in pitcher performance following a high pitch count outing. In this article, we will investigate whether PAP^3 has any value in predicting which pitchers are subject to injury, and if not, whether any PAP-style metric can be derived that does have predictive value.
Before claiming any success for any measure in predicting injury, we must fundamentally recognize that any PAP-style metric will be positively correlated with raw pitch counts. Pitchers with high pitch count totals will tend to have high PAP totals. If a PAP function provides no additional insight into which pitchers will be injured that pitch count totals alone, there is no reason to add the added complexity of a PAP system to our sabermetric arsenal. Only if a PAP function provides injury information above and beyond what can be learned from aggregate pitch counts should we consider it successful.
As with the previous study, I looked at starts for all pitchers between 1988-98 for which there was pitch count data in the Baseball Workshop/Total Sports database. The approach I used was to identify starting pitchers who suffered major injuries during that span, and compare them to comparable pitchers who did not suffer a major injury. Pitcher injury data was taken from Neft & Cohen's The Sports Encyclopedia: Baseball 2000.
In the annual season summary section of TSE:BB 2000, team rosters are presented, and a notation is made if a player was injured for more than 30 days. For the purposes of this study, I selected pitchers who were starting pitchers in the year they were injured, and whose recent history indicated a pattern of starting pitching. Generally speaking, if a pitcher was a full time or near-full time reliever in either of the two seasons prior to the injury, he was excluded from consideration. Pitch counts from relief appearances were not included for any pitcher, since relief outings are generally low in total pitch counts, and the hypothesis under consideration is that it is high pitch counts that overextend pitchers, and lead to injury risk.
Furthermore, only certain types of injuries were considered. A two-letter code indicated the type of injury (if known). Since pitcher overwork would most often be associated with arm injuries, the only injury categories included were shoulder injury, elbow injury, arm injury, and sore arm. Any injured pitcher with one of these codes was presumed to have injured his pitching arm (the reference does not specify which arm). Note that this categorization considers only the most serious arm injuries, namely those which held a pitcher out of action for a month or more. Less serious injuries, including missed turns in the rotation, and DL stays of less than 30 days, are ignored (and in fact, these pitchers are considered "healthy" as they did not miss 30 or more days due to injury during the season).
Since I wanted to consider pitchers for whom we had pitch count data for most of their career, any pitcher under consideration who accumulated more than 100 innings in the majors prior to 1988 was excluded.
Note that minor league pitch counts are not widely available at present, and while a more thorough treatment of the impact of career usage and pitch counts on pitcher injury susceptibility would certainly include them, I restricted the investigation to major league pitch counts only.
Finally, several pitchers appeared on the injured list multiple times during their career. Physiologically, prior injury makes one prone to future injury. To account for this, only the first season a given pitcher suffered a major injury is included in our data.
Using these criteria, a total of 73 injured pitchers were identified.
In order to identify a set of similarly worked pitchers who had not been injured, I found matches for each injured pitcher's age and career pitch count total. By doing so, I would have several pitchers with similar age and usage profiles, but who had not been injured. More specifically, for each injured pitcher, I found all pitcher whose careers through the same age had amassed within 10% or the injured pitcher's career pitch count total. That is, if a 25-year-old Jason Bere had about 7800 career pitches in 1995, I matched him with any other 25-year-old pitcher who had between 7020 and 8580 career pitches.
Of course, a further restriction was that any matching pitcher was not one of the 73 injured pitchers, even if they were injured at a different age than the one they were being compared for. If a single pitcher-season matched more than one injured pitcher, the duplicate entries were removed, so that no pitcher-season was counted more than once. A total of 569 healthy comparable seasons were identified, for an average of 7.8 healthy comparables per injured pitcher.
Note that the term "comparable pitcher" refers only to the aggregate number of pitches thrown in a pitcher's starts, not necessarily in the results. Two 27 year old pitchers with 5000 career pitches would be considered comparable in terms of workload, even if one had a 3.00 ERA, and the other a 5.50 ERA. They are comparable in the total amount of work performed (pitches thrown), not the in value of the results.
Career PAP as a Predictor of Injury
Our initial hypothesis is that PAP^3 has predictive power beyond raw career pitch count totals in assessing the likelihood of injury for major league pitchers. To test this hypothesis, I plotted career PAP^3 vs. career pitch counts for all the pitcher-seasons in the sample, which is shown in the chart below:
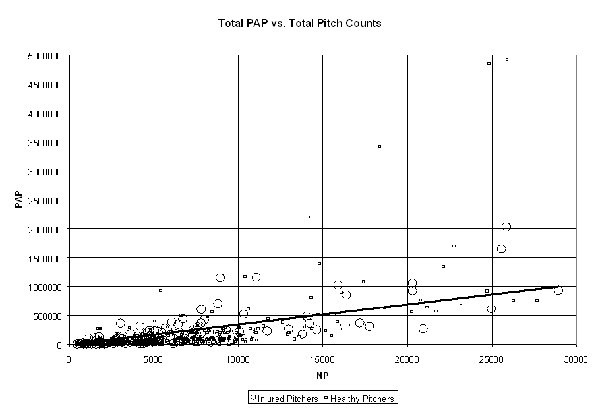
(Click for full-size image)
Over the course of any pitcher's career, he will invariably pick up PAP in some fraction of his outings. By looking at the usage patterns of many pitchers over the years, you can ascertain the "typical" amount of PAP a major league pitcher would accumulate given their pitch counts. Linear regression is one technique for mathematically determining what this typical PAP level is. The best fitting linear regression equation is plotted in the chart above as the solid line.
If pitchers with greater than usual PAP are more likely to be injured, we would expect more of the large dots indicating injured pitchers to lie above the trend line in the chart above. It's difficult to tell from visual inspection whether this is the case or not. We can, however, analyze to the data itself to see if this is true. Looking at the percentage of each group of pitcher that lie above the trendline, we discover that:
- 31% of all injured pitchers had above average career PAP totals for their career pitch counts.
- 9% of all healthy pitchers had above average career PAP totals for their career pitch counts.
This suggests that high PAP pitchers are more than three times as likely to be injured as low PAP pitchers of who've thrown similar numbers of pitches. We have our first piece of evidence that PAP provides predictive information beyond what pitch counts alone can tell us.
As a side note, the careful reader will note that there are four data points that exceed a career-to-date PAP total of 2,000,000. These four pitcher-seasons are all from the same pitcher, and far exceed the workload amassed by any other pitcher. This workhorse is, of course, Randy Johnson, whose career workload looks like a mistake in the chart. Whatever the results of our analysis of PAP and injuries, Johnson is almost certainly an extreme outlier, a remarkable physical specimen for whom comparison to regular major league pitchers may not apply.
Though we now have some indication that high PAP totals are a predictor of injury risk, the results are somewhat buried in the statistics. They key element of the findings above is that more PAP for any given number of pitches leads to higher risk. This leads to the concept of using PAP/NP as a measure of how intense or stressful a pitcher's pitches have been. I'll refer to PAP/NP as "Workload Stress" or simply "Stress".
I determined career-to-date Stress factors for each pitcher in our sample, with the intention of plotting Stress versus rate of injury. However, since each pitcher in the sample has an injury value of either 0 (healthy) or 1 (injured), a straightforward plot of points would not be particularly revealing.
What I did instead was sort the list of all pitchers by Stress factors, and created a moving average or "sliding window" of 50 data points at a time. That is, I took pitchers 1-50 as one data point, pitchers 2-51 for the 2nd data point, 3-52 as the third, and so on, such that with every step I was adding one pitcher with a high Stress factor, and dropping the one with the lowest Stress. I averaged the Stress factors for every pitcher in the window, and computed the percentage of pitchers in the sample who were injured. This creates a sample within the sample, for which we can estimate the injury rate for pitchers with Stress factors similar to the sample's average Stress. The results are below:
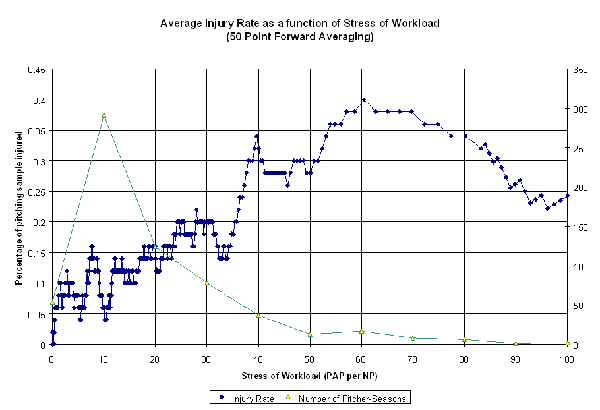
(Click for full-size image)
Here we see a more compelling representation of the relationship between PAP and injuries. There's a clear trend between Stress and the percentage of pitchers who get injured. There's a relatively constant increase between 0 and 50, with a leveling off thereafter. Over a quarter of pitchers with career Stress factors above 40 have suffered a major injury at some point during the time of the study, compared with less than 15% of those with career Stress factors below 20.
Interestingly, there are indications of a decline as you approach and exceed a Stress factor of 100 (the chart is truncated at Stress=100 due to lack of sample size above this level). However, the injury rate is still well above that of any Stress factor less than 40. Given the small number of pitchers in the upper ends of the chart, it could be a sample size effect. If we assume, for the sake of argument, that this decline is not simply random fluctuation, I would speculate that this represents a survival effect of sorts. The pitchers who can sustain that high a workload stress are those whose managers have pushed them harder and harder until they get a reputation as a workhorse who can consistently shoulder 130 pitch count outings. It takes awhile for both the pitcher to develop to a point where he can be effective in the late innings (and hence won't be pulled for a reliever). Also, a manager may be cautious with a new arm until he's comfortable enough with a pitcher to "know" how far he can go. Thus, the pitchers who end up with the highest levels of stress are the quality arms who've survived the weeding out process.
The Injury Likelihood Equation
The shape of the line on the chart, with a steeper slope at the beginning and leveling off as you go higher, suggests a logarithmic curve. An example of such a curve is shown below:
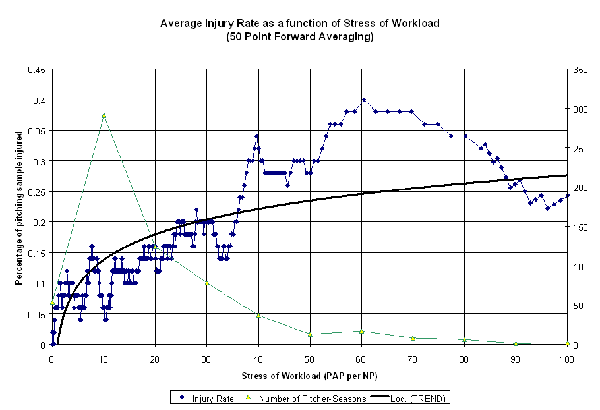
(Click for full-size image)
The formula for the trend line shown above is (LN() is the natural log function):
Prob(Injury) = 0.06 * LN(Stress)
Or, equivalently:
Prob(Injury) = 0.06 * LN(PAP/NP)
(Technical note: This equation holds for Stress factors greater than or equal to 1. The curve is equal to zero for Stress factors below 1).
What this chart suggests is that a pitcher's career stress factor can help predict the likelihood of that pitcher suffering a major arm injury at some point during his career. For example, a pitcher who's consistently around a Workload Stress of 30 has a 20% chance of missing a month or more due to arm injury at some point in his career.
Statistical Significance of Results
Having derived these apparently impressive results, it's only prudent to ask whether they are statistically significant or not. One commonly used statistical test is called a Chi-squared test. Though the details of the test will be omitted here, for our purposes, the Chi-squared test determines the likelihood that the results we've seen could result from a random split of a uniform population, given the sample sizes. In other words, Chi-squared will check the possibility that the high and low PAP pitchers are actually equally likely to be injured, and the observed differences are due to chance (this is what's called the "null hypothesis" — that PAP has no predictive value). If the resulting probability from the Chi-squared test is too high (traditionally around 5%), then we can't reject the possibility that the null hypothesis is true, meaning that the differences could be explained by chance rather than due to any predictive power of PAP. Conversely, a very low probability result from the Chi-squared test increases our confidence that the results are not due to chance, and that separating pitchers based on PAP does provide information about their relative injury risks.
Turning first to the career PAP totals, we noted that pitchers with above average PAP totals given their career pitch counts were far more likely to have been injured than pitchers with below average PAP totals. Computing a Chi-squared probability for this sample indicates that the split has only a 0.000018% chance of having occurred by chance. This easily passes the criteria for statistical significance.
Looking then at the Workload Stress factor versus (PAP/NP), I took a more granular approach, dividing the sample space into quintiles by PAP/NP, and computed the injury rates in each of the five groups. I then computed the Chi-squared probability of this split occurring by chance. The result were comparable to our previous findings — a relationship like the one observed has a miniscule 0.0000028% chance of happening by chance. Again, the Stress Workload factor clears the bar for statistical significance.
As with the short-term PAP results, I examined other possible PAP formulae to see if the relationship to injury risk was noticeably stronger. Though I do not present the charts here, I tested classic PAP, other polynomial versions of PAP (e.g. PAP = (NP-100)^2), and varying the baselines (100 pitches, 90 pitches, 110 pitches, etc). There was no dominant winner among the various formulae. In general, they resulted in similar predictions as PAP^3. Perhaps isn't that surprising, given that unlike single starts, usage patterns tend to even out more over the course of a career. Furthermore, even with the results we have, predicting injury is an inexact science, and Workload Stress factors are no guarantee for either health or injury. Therefore, any reasonable metric that gives extra weight to high pitch count outings should yield a risk factor that is in the same ballpark as PAP^3 (pardon the pun). Given that we have a preferred metric for short-term impact that does acceptably for long-term injury risk as well, we will stick to simplicity, and use a single metric for both purposes. The PAP^3 formula will be the basis for our Pitcher Abuse Point work going forward.
Though career Workload Stress has been shown to, we can compute Stress factors for individual pitching seasons (or groups of seasons) to assess whether a pitcher is "on pace" for difficulties. The list below shows the pitchers with the highest and lowest Workload Stress rates for the 2000 season (minimum 10 games started):
PITCHER GS PAP NP STRESS Hernandez,Livan 33 422979 3825 110.6 Johnson,Randy 35 439098 4021 109.2 Schmidt,Jason 11 101865 1203 84.7 Helling,Rick 35 313875 3791 82.8 Villone,Ron 23 150263 2246 66.9 Leiter,Al 31 229252 3478 65.9 Clemens,Roger 32 218043 3433 63.5 Hitchcock,Sterling 11 70714 1127 62.7 Wolf,Randy 32 217292 3528 61.6 Martinez,Pedro 29 190327 3165 60.1 Elarton,Scott 30 188275 3139 60.0 Appier,Kevin 31 194467 3314 58.7 Davis,Doug 13 78320 1338 58.5 Miller,Wade 16 97914 1724 56.8 Suppan,Jeff 33 181089 3488 51.9 Mussina,Mike 34 183194 3657 50.1 ... Dreifort,Darren 32 4498 3114 1.4 Karl,Scott 13 1339 1037 1.3 Yan,Esteban 20 2262 1801 1.3 Garland,Jon 13 1407 1198 1.2 Romero,J.C. 11 1009 961 1.0 Glynn,Ryan 16 1512 1456 1.0 Halladay,Roy 13 1253 1208 1.0 Rose,Brian 24 1728 1862 0.9 Blair,Willie 17 1342 1545 0.9 Guzman,Geraldo 10 737 896 0.8 Perez,Carlos 22 1531 1921 0.8 Ohka,Tomo 12 793 1096 0.7 Rupe,Ryan 18 757 1553 0.5 Bergman,Sean 14 512 1152 0.4 Gooden,Dwight 14 343 1161 0.3 Fassero,Jeff 23 152 1883 0.1 Schourek,Pete 21 126 1731 0.1 Cornelius,Reid 21 126 1828 0.1 Irabu,Hideki 11 27 853 0.0 Halama,John 30 63 2607 0.0 Arroyo,Bronson 12 8 958 0.0 Johnson,Mike 13 8 981 0.0 Stottlemyre,Todd 18 1 1496 0.0 Eiland,Eiland 10 0 667 0.0
Injuries to a key pitcher can have a devastating effect on a team's fortunes, not to mention that they can shorten or hinder a pitcher's career. With escalating salaries, proper pitcher usage is increasingly important to maximizing a team's investment in its personnel. As a result, pitch counts are in prominence, managers and pitching coaches are scrutinized more closely in how they handle a staff, and player development systems in the minors are increasingly aware of protecting young arms.
The research presented here has shown, in essence, that not all pitches are created equal. It is the high pitch count outings that represent the greatest risk for both short-term ineffectiveness, and long-term potential for injury. The PAP^3 system represents the most comprehensive attempt to date to quantify the impact of starting pitcher usage over both time horizons, allowing us to estimate, based on empirical evidence, the tradeoffs of having a star pitcher throw deep into a game.
However, before placing too much weight on these discoveries, some caveats apply. The results of this study should not be considered final because many active pitchers are included in the study. It will be several years before a large sample of pitch counts for entire pitcher careers becomes available, and such a resource is necessary before we can complete the analysis has been started here.
It's important to note that the Workload Stress factor is not a prediction of injury risk for a specific season, but rather a risk of injury over several years of pitching at that level. Also, PAP^3 may underestimate the relationship between high pitch counts and injuries. This study considered only the most major injuries, and did not look at minor injuries, missed turns in the rotations, or shifts from starting to relief pitching. We also proceeded assuming that the injury effect of high pitch counts would manifest itself in arm problems. It's possible that there would also be effects for other kinds of non-arm injuries (especially back and leg injuries).
The research questions are far from resolved, and there are still many facets to the problem that have yet to be fully addressed. For example, a pitcher's age may be of considerable importance when assessing the risks of specific pitch count limits, but was not included in this study. Important data is still missing from the study, such as minor league, spring training, and post-season pitch counts. The interactions and spacing between pitcher outings may prove to have a significant effect — does starting on 3 days rest vs. 4 days rest substantially affect the risk of either injury or ineffectiveness? There may yet be better estimates of injury risk as I did not conduct an exhaustive search for all mathematical representations, favoring the simplicity of a single measure like PAP^3. Biomechanical experts may help identify physical characteristics that indicate which pitchers are more or less susceptible or have greater endurance, allowing personalized PAP formulae for individual pitchers.
There is also the possibility that the relationship between pitch counts and injury risk is not static over time. Improved training methods, changing usage patterns and strategies, new medical technology and techniques, new diagnostics and screening could all impact the negative effects of high pitch counts. Pitch count data from 1950 may not be terribly informative about the effects on modern pitchers. Similarly, twenty years from now, an entirely different PAP formula may need to be developed to take into account the impact of a machine that rejuvenates muscle tissue instantly that some scientist has yet to discover. Clearly, we have not learned all we need to know about the effects of pitcher usage.
For now, however, we can confidently say that PAP^3 yields information about pitcher performance and durability not answered by pitch counts alone under current playing conditions. Long pitch count outings noticeably decrease expected short-term performance, and high stress workloads over time increase the chances for serious injury. Any strategic analysis of pitcher usage will have to consider the tradeoff between winning the current game and the long-term cost. There are clearly times when you will want to ride a workhorse hard, such as a key playoff game (though Al Leiter will attest that there are limits even in the World Series). Finding the right balance between winning now and winning tomorrow remains a interesting challenge, and today we have another tool in our arsenal to assess a team's sustainable pitching strategy.
I'd like to thanks Dr. Lutz Mueller of Lumina Decision Systems for his advice and consultation on the design and statistical testing methods in this research.
Thank you for reading
This is a free article. If you enjoyed it, consider subscribing to Baseball Prospectus. Subscriptions support ongoing public baseball research and analysis in an increasingly proprietary environment.
Subscribe now