
Traducido por Carlos Saiz Domínquez
Uno de los principios clave de la Sabermetría es que 10 carreras equivalen, aproximadamente, a una victoria. El ex editor jefe de BP, Ben Lindbergh, escribió esto en su artículo de 2013 en Grantland sobre la magia del encuadre de Jose Molina:
…Molina ha salvado a sus equipos 111 carreras -o, usando la conversión estándar de 10 carreras a una victoria, alrededor de 11 victorias- debido a su encuadre entre 2008 y 2013.
Diez carreras para ganar pueden ser estándar, pero seguro que no es intuitivo. ¿Necesitas 10 carreras para ganar un partido? Los equipos anotaron 10 o más carreras en un partido sólo 422 veces el año pasado. Eso es menos del nueve por ciento de todos los partidos Y ganaron 405 de esos partidos, un porcentaje de victoria de 0.960. ¿Por qué necesitas 10 carreras? ¿Por qué no siete? Los equipos que anotaron siete carreras ganaron el 83 por ciento de las veces. ¿O seis? Esos equipos ganaron el 72 por ciento de sus partidos. O cinco: 62 por ciento. Cuatro es la línea divisoria; los equipos que anotaron cuatro carreras en 2017 perdieron más de la mitad de sus partidos. ¿Pero por qué 10? Son dos veces cinco, y los equipos que anotan cinco ganaron casi dos tercios de las veces.
La razón es matemática. La ecuación de regresión básica es y = mx + b. Lo que intentas predecir, y, se puede expresar como una m multiple (la pendiente) de los datos que tienes, x, más una constante, b (la intersección). Por ejemplo, si está convirtiendo Celsius a Fahrenheit, la ecuación es F = 1.8C + 32. La variable que está tratando de modelar, grados Fahrenheit, es igual a un múltiplo de 1.8 veces el punto de datos que tiene, grados Celsius, además de una constante de 32. Si está de vacaciones en Canadá y escucha que el máximo será de 25, use mangas cortas, es decir 1.8 x 25 + 32 = 77 para los estadounidenses.
Esa es una ecuación exacta. Por lo general, las ecuaciones de regresión no son exactas, pero te acercarán bastante al número deseado. Así que voy a usar la regresión para predecir las ganancias basadas en el diferencial de carreras. Los Indians tuvieron el mejor diferencial de carrera en las Grandes Ligas el año pasado, en +254 (818 anotadas, 564 permitidas). Ganaron 102 partidos. Los Padres tuvieron el peor, con -212 (604 anotadas, 816 permitidas). Ganaron 71. Los Indians no ganaron la mayor cantidad de partidos en las Grandes Ligas (fueron los Dodgers con 104), pero estuvieron cerca. Los Padres no fueron los que menos partidos ganaron en las mayores (los Gigantes lo hicieron, 64), pero estuvieron cerca.
Revisé cada equipo para cada temporada desde 1901, cuando se formó la Liga Americana. Eso me dio 2.468 temporadas de equipo. Para cada uno, calculé el diferencial de carrera (mí x) y las ganancias del equipo (mí y). Luego utilicé el software de regresión lineal de Excel (no esperabas que lo hiciera a mano, ¿verdad?) para generar una fórmula de regresión. Esta es:
Victorias = 0.103 x diferencial de carreras + 78.2
Mirando sólo la primera cifra, cada carrera te da 0.103 victorias más. Da la vuelta eso, y obtienes que una victoria es igual a 1 /. 103 = 9,74 carreras. O unas 10 carreras. Cada 10 carreras adicionales anotadas, en relación con las carreras permitidas, equivalen a una victoria.
Bien, todo el mundo, podéis volver a uniros ahora. Hemos establecido que, en promedio desde 1901, cada 10 carreras adicionales que los equipos han anotado (o, de hecho, prevenido) les ha dado una victoria extra. Eso no significa que tengas que anotar 10 carreras para ganar. Se dice que después de 117 temporadas en las que participaron 2.466 equipos, cada 10 carreras extras que un equipo anota en relación a las carreras que permite, le sirve para añadir una victoria más. Pero no es un número inmutable. El equipo promedio anotó 5.14 carreras por partido en 2000. Doce años antes, el equipo promedio anotó exactamente una carrera menos por partido. Seguramente el número de carreras extras necesarias para conseguir una victoria no era el mismo en 1988 que en 2000, ¿verdad?
Sí, fue diferente. Que 10 (o, más exactamente, 9.74) carreras por partido es un promedio a largo plazo. Pero varía ¿Cuánto varía? Para responder eso, calculé la relación de regresión (descrita en los párrafos que algunos de ustedes omitieron) para cada año entre 1901 y 2017. Aquí hay un gráfico que muestra la cantidad de carreras adicionales netas que equivalieron una victoria en esos años
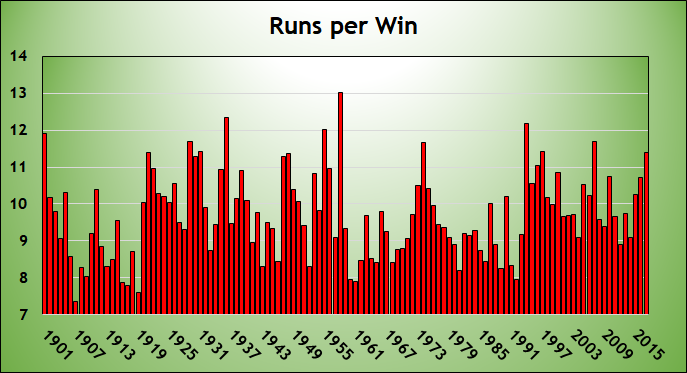
En 1988, cuando los equipos anotaron 4.14 carreras por partido, 8.89 carreras adicionales por temporada equivalieron a una victoria extra. En 2000, cuando los equipos anotaron 5.14 carreras por partido, una victoria extra suponía 10.86 carreras. Entonces, sí, las carreras por victoria varían de acuerdo con el entorno de puntuación.
Aquí está el mismo gráfico, pero agregué carreras por equipo y por partido como una línea negra. La escala está en el eje derecho. Como puede ver, mientras que las barras rojas son un poco ruidosas, cuanta más puntuación, más carreras se requieren por victoria.
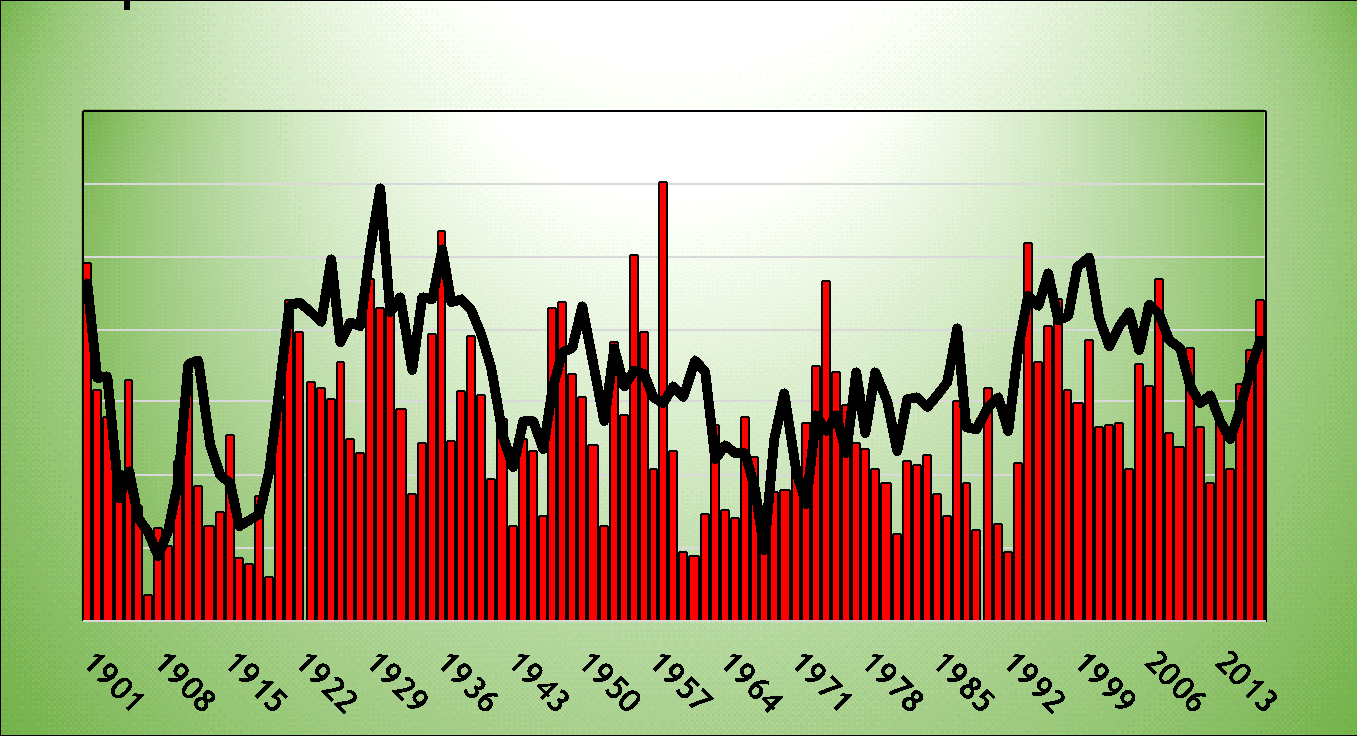
La correlación entre carreras por partido y carreras por victoria es 0.61. ¡Eso es bastante alto! Significa que cuantas más carreras se anoten, más carreras se necesitan para obtener una victoria extra. Eso tiene sentido, ¿verdad? En 1968, el Año de los Pitcher, los equipos anotaron solo 3.42 carreras por partido. En 1930, la Liga Nacional bateó .303/.360/.448 y los equipos anotaron 5.55 carreras por partido. Así que obviamente, necesitabas más carreras para asegurar una victoria en 1930 que en 1968. Y lo sabes porque usaste la fórmula anterior: 11.3 carreras en 1930, 8.4 carreras en 1968
Así que estás en lo correcto, en promedio, si haces las siguientes matemáticas mentales, 10 carreras equivale a una victoria. Pero si quiere ser realmente preciso, debe ir más allá y observar el entorno de puntuación. Si dijiste “10 carreras por partido” en 2012, te pasaste por una carrera completa. Si lo dijiste esta temporada pasada, te quedaste corto por más de una carrera. Como con muchas cosas en la Sabermetría y en la vida, son relativas.
Thank you for reading
This is a free article. If you enjoyed it, consider subscribing to Baseball Prospectus. Subscriptions support ongoing public baseball research and analysis in an increasingly proprietary environment.
Subscribe now