One of the classic managerial dilemmas–perhaps the classic managerial dilemma–is whether to remove a starter who is still throwing pretty well for a middle reliever in the sixth, seventh or eighth inning. This decision is relatively straightforward if the sole concern is winning the game in question. You trot your butt out to the mound, the pitcher grabs his crotch a couple times and spits out his chaw and tells you that his arm still feels real good, and then you sit back down in the dugout ask the pitching coach what’s really going on. If the pitching coach tells you that the guy throwing in the bullpen is likely to be more effective than the starter, you make the switch. Otherwise, you leave the dude out there. Certainly, it’s possible to make an error of judgment now and then–figuring out just how much fatigue will reduce a pitcher’s effectiveness is a guessing game of sorts–but fundamentally, the problem is simple.
Things become much more complicated if you are concerned not only about the outcome of the current game, but also the outcomes of future games. If your ace has given you a 8-0 lead after seven innings with a pitch count of 110 or so, common sense dictates that you pull the guy before the eighth. You sacrifice some very small amount of expectation in the near-term if you replace him with an inferior alternative–maybe you’ll win 99.68% of the time instead of 99.72%–but the future benefit of keeping him healthy and well-rested for subsequent outings well outweighs this.
It isn’t always that easy, though, especially in the post-season when pitchers are frequently asked to throw high-pressure innings against good offenses on short rest. Nor is the impact on future games easy to determine. If Roy Oswalt is going to be marginally less effective in Game 5 because he went an extra inning in Game 2, how much will that impact Houston’s probability of winning the ballgame? How much should the impact on Game 5 be discounted since there might not be one at all?
Those questions are vexing to answer, but we can try and quantify the impact that removing a better pitcher for a worse one will have on a game whose outcome is in immediate doubt. Let’s take Ron Gardenhire’s decision to remove Johan Santana in Game 1 of the ALDS as an example. Santana, in spite of a thin, two-run lead and the appearance of having plenty left in his tank, was pulled in favor of Juan Rincon after seven innings and 93 pitches. Rincon, it is true, had a pretty good season, but was not quite as good as his ERA suggests, and nothing along the lines of a post-All Star Break Santana; the Twins were giving a little something up by making the switch. For purposes of this problem, let us assume the following:
- Santana’s “true” ERA against an average lineup is 2.00.
- Rincon’s “true” ERA is 3.50.
- Joe Nathan, who will pitch the ninth regardless of what happens in the eighth, has a “true” ERA of 2.50.
In other words, the Twins’ disadvantage stems from displace one inning of 2.00 ERA pitcher with one inning of 3.50 ERA pitcher. How much does this reduce their chances of winning the game?
Our model needs to take into account the following:
- The game score and situation (thanks, Cap’n Obvious)
- The quality of the opposing offense
- The distribution of run scoring for a pitcher with a given ERA.
It’s that latter point that gets a bit complicated. We can figure that if Santana has a 2.00 ERA, and Rincon has a 3.50 ERA, the difference between the two is 1.5 earned runs per game, or 1/6th of a run per inning if we divide that figure by nine. So now we project the final score to be: Twins 2, Yankees 0.16666667.
Not very helpful, right? What we really need is a distribution. By that I mean: how often will a pitcher with a 4.00 ERA give up two runs in an inning? How often will a pitcher with a 3.35 ERA pitch a shutout inning? How often will the Angels put up a five-spot against Nate Cornejo? Stuff like that.
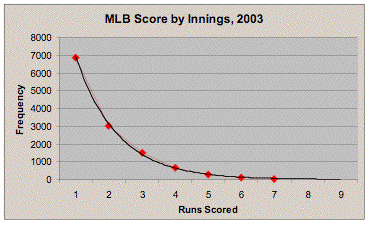
As a starting point, I looked at the distribution of run scoring across all major league half-innings in 2003.
Runs scored by one club in an inning, MLB 2003 Runs Scored Frequency Percent ------------------------------- 0 30922 71.1% 1 6845 15.7% 2 3011 6.9% 3 1507 3.5% 4 670 1.5% 5 305 0.7% 6 117 0.3% 7 62 0.1% 8 12 0.0% 9 6 0.0% 10 6 0.0% 11 0 0.0% 12 1 0.0% 13 1 0.0% 14 1 0.0%
MLB teams, in the current run environment, score one or more runs in a frame around 30 percent of the time. I suspect that most of you, if asked to guess at the figure before seeing the data, would have estimated something reasonably close to that. Multiple-run innings are rare, occurring 13.2% of the time. An inning of five or more runs comes up once every five games or so.
One interesting property is that the run scoring distribution appears to be governed by an exponential decay function:
By that I mean, the ratio of four-run innings to three-run innings is approximately the same is the ratio of three-run innings to two-run innings, the ratio of two-run innings to one-run innings, and so forth. We’ll call this number g, for Golden Run Ratio. The ratio of one-run innings to scoreless innings is not the same as the rest–runs tend to come in bunches, and it’s a lot harder to score the first one than the second–but conveniently enough it works out to be almost exactly twice as large as the other ratios, or 2g.
I’ll skip describing the algebra and the fancy Excel trickery that this involves, but as it works out, it is possible to pick an appropriate number g–a Golden Run Ratio–that fits any particular level of offensive output that we might want. For example, for a team that scores 5.0 runs per game, the “correct” g is 4.33. For a team that scores 3.0 runs per game, g is 5.64. Lower run-scoring outputs are associated with higher Golden Run Ratios, and the larger that g is, the larger the ratio of 0-run innings to 1-run innings (implying more shutout innings), 1-run innings to 2-run innings (implying fewer multi-run innings), and so forth. Here, for example, are the estimated run-scoring frequencies for teams scoring 3.0, 5.0 and 7.0 runs per game, as well as the actual run-scoring distribution in 2003 (MLB teams scored roughly 4.8 runs per game last year).
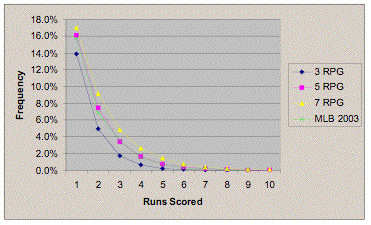
I should point out that I haven’t validated the run scoring ratios empirically–it’s possible that the curve takes on a somewhat different shape at very high or very low levels of run-scoring output–but the relationship is elegant enough and organic enough that I’m comfortable with it. (Sign of the apocalypse: a stathead starts talking about how a ratio pleases him aesthetically).
This has been quite a grand diversion–the Yankees have scored 36 runs off Curt Schilling in the time that I’ve been writing this–so let’s get back to the problem at hand. The Yankees have a good offense, averaging 5.52 runs per game versus almost exactly 5.00 for the league as a whole, and we need to account for that in our analysis. After using a version of the log 5 formula and making an adjustment for unearned runs, we figure that they’ll score about 2.37 RPG against Santana, 4.15 against Rincon, and 2.96 against Nathan. Here are what the Yankees’ run distributions look like against Ron Gardenhire’s eighth-inning options:
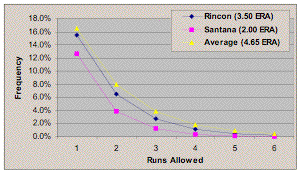
New York will score one or more runs 26.7% of the time against Rincon, versus 18.2% of the time against Santana–roughly a 50% increase. They’ll score two or more runs 11.2% of the time against Rincon, and 5.6% of the time against Santana, or almost exactly twice as often.
We also need to know about the Twins, since they’ll have a chance to add to their lead in the ninth, but with Mariano Rivera warming up (we’ll figure him for a 2.00 ERA) and an mediocre offense, they figure to score at a level of just 2.06 RPG against him, which results in their getting shut out on the inning 83.5% of the time.
All of this corresponds to the Yankees winning 13.1% of the time if Rincon pitches the eighth, and 8.9% of the time if Santana pitches the eighth. In other words, pulling Santana early will cost the Twins the game 4.2% of the time, or about one time in 24. (I have skipped some tedious steps here involving mapping win probabilities to run scoring distributions, but the procedure is simple and should be accurate, provided that our assumptions are correct. For the sake of completeness I will mention that I assume that the game is a coin-flip if it goes into extra innings tied.)
One time in 24? Is that chance worth taking for the opportunity to preserve Santana’s arm strength for Game Four? Well, I’ve already said that I wasn’t going to try and come up with a definitive answer to that part of the equation, but I owe you guys at least a guess, grain of salt and all.
Let’s assume that the Twins will face an opposing Yankee starter with a 4.00 ERA for the first seven innings of Game Four, and relief pitchers with a 3.00 ERA for the last two innings of Game Four. Let’s further assume that:
- If Santana doesn’t pitch the eighth, he will avoid being fatigued and throw 7 innings at a 2.00 ERA level in Game Four. Relief pitchers with a 3.00 composite ERA will pitch the last two innings.
- If Santana does pitch the eighth, he will pitch six innings at a 2.25 ERA level of performance. Relief pitchers with a 3.00 composite ERA will pitch the last three innings.
We throw these numbers into the model I’ve just described and come up with the following:
- The Yankees have a 33.5% chance of winning Game Four against a rested Santana.
- The Yankees have a 37.1% chance of winning Game Four against a fatigued Santana.
That works out to a 3.6% difference, which is close enough to the margin of error to let Gardenhire off the hook. Are those numbers reasonable? Keith Woolner and Rany Jazayerli’s research in Baseball Prospectus 2002, which I’m oversimplifying here, suggests that a tired pitcher can expect to experience an ERA increase of somewhere between 2% and 5% from his baseline level in his subsequent outings, so the 12.5% increase we’ve predicted for Santana looks to be a little out of line. On the other hand, it’s easy to imagine that the effects of fatigue will be much amplified on short rest, and expecting any pitcher to maintain a 2.00 ERA in this day and age requires him to be more or less mechanically flawless. I don’t think my estimate is unreasonable, and I don’t think that Gardenhire’s decision was obviously wrong, In general, you never want to do anything that reduces your chances of winning in a high-leverage situation in a high-impact game, though if it could effect the course of six or seven innings in a subsequent game of equal importance, the decision may be defensible. (Though, as Joe Sheehan points out, the option of replacing Santana with Rincon was strategically dominated by having Joe Nathan go two innings instead).
You may also detect some tension between our sometimes advocating for aggressive use of pitchers during the post-season and our strongly-expressed distaste for pitcher overuse during the regular season. But both cases are simply a matter of a team maximizing its utility. According to Clay Davenport’s figures, winning Game One of an LDS will increase a team’s chances of winning the World Series by somewhere in the neighborhood of five percent. Whether that seems like a lot or not I don’t know, but it’s surely many magnitudes of order larger than the corresponding percentage increase from winning an additional regular season game. I recognize that there’s an ethical component to preventing pitcher abuse that shouldn’t be dismissed, but the soundest argument rests in strategy. What is the loss in World Series win percentage that the Cubs suffer if Mark Prior‘s risk of catastrophic injury increases from 3.2% to 4.0% as the result of a 135-pitch outing? Probably somewhat larger than the marginal gain from having a marginally higher chance of winning a regular-season game, but considerably smaller than the marginal gain if it’s Game 7 of the World Series.
I’ll close out by providing benchmarks for some common situations that occur during the regular season. We’ll use the following assumptions in all our examples:
- The 2004 Cubs are hosting the 2004 Astros, with corresponding team-offense levels.
- Carlos Zambrano is on the mound and capable of continuing at a 2.75 ERA. The relief pitchers who would replace him are people like Kyle Farnsworth and will have a 4.00 ERA.
- The Cubs are facing league-average pitching against the Astros.
- The decision is between pulling Zambrano immediately and having him go exactly one more inning.
Scenario 1. Cubs have a four-run lead after six innings. Cubs’ chances of winning are 95.6% if Zambrano pitches the seventh and 94.5% if the bullpen does (1.1% reduction).
Scenario 2. Cubs have a three-run lead after seven innings. Cubs’ chances of winning are 95.0% if Zambrano pitches the eighth and 93.3% if the bullpen does (1.7% reduction).
Scenario 3. Cubs have a one-run lead after eight innings. Cubs’ chances of winning are 95.0% if Zambrano pitches the ninth and 88.2% if the bullpen does (6.8% reduction).
Scenario 4. Game is tied after six innings. Cubs’ chances of winning are 53.4% if Zambrano pitches the seventh and 51.0% if the bullpen does (2.4% reduction).
Scenario 5. Astros have a one-run lead after seven innings. Cubs’ chances of winning are 27.8% if Zambrano pitches the eighth and 26.4% if the bullpen does (1.4% reduction).
Certainly, some situations are more important than others, but it’s a real stretch to say that the entire game hinges on getting one last inning out of the starter, even when he is very good and the bullpen alternatives are pretty bad. But during the post-season, the mere chance that the outcome of the game depends on extending a starter is important enough that the strategic imperatives are profoundly different.
Thank you for reading
This is a free article. If you enjoyed it, consider subscribing to Baseball Prospectus. Subscriptions support ongoing public baseball research and analysis in an increasingly proprietary environment.
Subscribe now