During a May 14 chat session on ESPN.com,
Bill James referred to my research on catcher’s game-calling and pitcher-handling, and
his criticism of it. The research he refers to consists primarily of an article from Baseball Prospectus 1999 entitled
"Field General or Backstop?"
and a followup posted here on the BP Web site called
"Catching Up With The General."
Since the chat session, I’ve received dozens of e-mails asking for additional details. The response from BP readers finally
prodded me into finishing some related projects I’d had in progress for a while, which I’ll present later in this article.
Last summer, James was kind enough to send me a copy of an article (which I believe remains unpublished) called "Modelling
the Problem of Making Sense of Catcher ERAs," and we exchanged a series of e-mails discussing his findings. James created a
computer simulation in which catchers were assigned a "true" defensive value, and thousands of seasons were simulated
with a mix of pitching staffs. In each simulated season, the observed catcher’s ERA was determined from the simulated results,
and compared to the "known" catcher ability. The accuracy of the observed CERA’s was then determined.
His primary conclusion was that even if catchers do have a significant defensive ability, there will be too much variation from
year to year for CERA to be a reliable indicator of it. There’s additional detail and avenues of analysis that he takes in the
article as well, and I hope I haven’t misstated his work in the summary above, nor given away too much about an article not in
general circulation. Bill James wasn’t the first person to suggest a simulated approach to me after BP99’s publication, but his
was, by far, the most complete attempt at doing the work.
One of the key differences between our approaches is that James directly modeled CERA, considering only runs and innings played,
whereas my research used the weighted outcome of plate appearances to measure the differences between catchers. The former has
the advantage of directly measuring the desired result (run prevention); the latter has a greater sample size to work from
because it relies on plate appearances, but works on the events leading to run prevention (hits, walks, and outs), rather than
run prevention itself.
I’ve constructed a computer model that simulates pitcher/catcher interactions, similar in concept to James’s model, but designed
to measure catcher performance with the method I outlined in my original article (pitching runs per plate appearance, or PR/PA).
This is consistent with my goal of isolating "game-calling" or "pitcher handling"–the catcher’s impact on
the pitcher’s ability to prevent hits and walks–rather than his effect on the running game.
Within the simulation, I took the actual stats from every pitcher in 2001 who pitched at least 50 innings. For each pitcher, I
computed the likelihood of each batting event (single, double, triple, home run, walk, out) per plate appearance. Weighting each
probability by the Linear Weights coefficient for each event and summing yields the pitchers base PR/PA.
I then generated two catchers with their own game-calling ability, manifested as raising or lowering a pitcher’s ERA, which I’ll
call his CERA factor. The difference between the two catchers’ CERA factor was a parameter chosen to create a marginal impact on
the pitcher’s PR/PA. That is, a CERA difference of 0.25 (where a pitcher has an ERA of 4.50 with catcher A, and 4.25 with
catcher B) would be converted into an equivalent difference in PR/PA. I then scaled the combined pitcher/catcher PA outcome
probabilities to include the catcher’s effect.
For each pitcher/pair-of-catchers, I simulated two seasons with a random number of plate appearances (between 500 and 1,000 per
season), and split them between the two catchers (with the primary catcher getting between 50-80% of the PA). I simulated the
plate appearances for each catcher, totaled how many hits, total bases, walks, and outs occurred, and computed the observed
PR/PA. By comparing the observed difference in PR/PA to the "known" CERA factor (which was a parameter that fixed the
actual difference in ability between the two catchers), we can determine whether the results from the simulated seasons
accurately reflect whether catcher A was better than catcher B.
I tested 21 CERA factors: 0.01, 0.05, 0.10, and every five-hundredths of a run up to 1.00 (that is, testing catchers who had a
true ability to change a 4.00 ERA pitcher into a 3.99 ERA pitcher on the low end, or a 4.00 ERA pitcher to a 3.00 ERA pitcher on
the high end). I simulated 100 pairs of seasons for each pitcher, resulting in more than 60,000 simulated seasons per CERA
factor, or 1.2 million total seasons.
For the purposes of measuring ability, each pair of catchers had one "above average" and one "below average"
catcher. A successful result would simply be to see if the simulation correctly identified the above-average catcher. This is
similar to James’s approach.
I looked at four different (but related) measures of results for each CERA difference:
- Whether the results from year 1 and year 2 were consistent (both indicate a catcher is good, or both indicate that he’s bad)
- Whether the results from year 1 and year 2 were inconsistent (shows up as good one year, and bad the other)
- Whether both years yield the correct results (Years 1 & 2 match, and they correctly identify the true underlying ability of
the catcher) - The likelihood is that two consistent years of results correctly identify the catcher’s ability.
As you might expect, the likelihood of correct predictions goes up as the gap between the catchers increases, as shown in the
chart below:
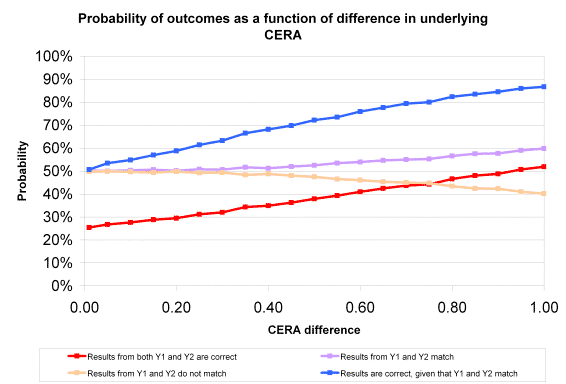
The most dramatic rise is in the confidence that matching results in two seasons indicates the right catcher. At a 0.01 CERA
difference, the odds of two years of matching results being correct is barely above 50%, or almost the same as flipping a coin.
However, if we know that there’s a 0.75 CERA difference between two catchers, and two years of results indicate catcher A is
better than catcher B, we can be about 80% certain that A is, in fact, the better catcher. It’s an artificial situation, knowing
what the gap between two catchers is, but not knowing which one of the two is actually the better one. But we need to know this
in order to assess the probability of correct observations later on.
We can see in the chart above some of the same results that James saw in his analysis. Even at a known gap of 1.00, there’s
still a 40% chance of getting mixed results (A is better one year, B the next), which give us no real indication which catcher
is better. Even worse, there’s an 8% chance of getting two false results (catcher A better in both years, but catcher B really
has the superior ability), and wrongly identifying the better defensive catcher. The chance of getting a truly unambiguous and
correct result is only about 52%, even at the highest levels of ability simulated.
Does this then mean that Bill James is correct, and that CERA isn’t a reliable indicator even if there is significant catcher
defensive ability? Let’s keep investigating before drawing any premature conclusions.
We’ve looked up until now at observing a single pitcher and catcher (or pair of catchers), and noted that it is difficult to
rely on one or two years of observation to detect even large differences in ability. Part of the model James sets forth, though,
is that catchers, as a group, have a range of abilities distributed in a bell curve with most catchers near the average, and
fewer outliers at the highest and lowest levels of ability. The next step in my model was to move from simulating seasons for a
given catcher, to a group of different catchers of differing ability and analyzing them as a whole.
In the next phase of the analysis, I generated 50,000 catchers with a randomly determined CERA factor (using a normal
distribution centered at zero, and a standard deviation of +/- 0.11 ERA, the same standard deviation used in James’s work). Note
that this is different than in step one, as each iteration of step one used a catcher ability of a fixed and known size. Here,
we are varying the mix of catchers in a random way, according to one hypothesis about how talent might be distributed.
I created a probability distribution for getting correct or incorrect results in two seasons using the results for each CERA
factor from step one. I modeled how likely each catcher was, over two seasons, to produce matching or mixed results, and whether
matching results were correct.
Using a 0.11 CERA talent distribution, the results are not remarkable–about 49.73% of the catchers produced mixed results over
two years, 26.83% produced two correct results, and 23.45% produced two incorrect results. Perfect randomness would be expected
to produce 50%/25%/25%, so there’s a just a very slight tendency towards getting the two correct results. That’s still not
compelling evidence that this range of CERA ability would be detectable.
Up until now we’ve only been considering the "sign" of the catcher’s ability–that is, whether he’s a positive or
negative influence on the pitcher’s performance. We haven’t used the magnitude of the observed differences to help us understand
the problem in more detail. (I should note that part of Bill’s article does look at extreme observed results, but the following
discussion goes in a different direction than his line of inquiry).
Across large groups of similar catchers, some trends may be discernable if an ability exists. Specifically, if you look at a
large number of catchers who registered as below average in year 1, and a true ability exists, then the average observation in
year 2 should be lower than average, even if the year-to-year variation for individuals is very high. Similarly, the top echelon
of catchers from year 1 should post an above-average collective performance in year 2. Conceptually, it makes sense, but
reality, of course, could be different. Should such an effect be detectable, or will the noise obscure the underlying signal, as
it did with the per-catcher analysis?
I took the 50,000 of the simulated catchers and divided them into 4 quartiles (numbered 0-3, just to be confusing), according to
their year 1 observed results. The 12,500 catchers who rated lowest in year one formed one quartile, the next 12,500 formed the
second quartile, and so on. The average year 1 performance for each quartile were, as expected, quite different, as they were
grouped on this basis:
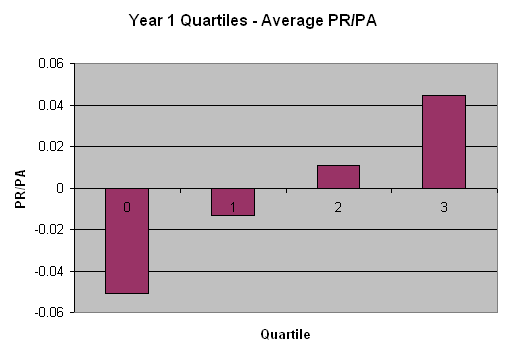
The second step is to look at how each quartile did in year 2. Since we know that the underlying simulation included a catcher’s
ability component, if the statistical noise is too great, we should not expect to see a chart resembling the one above, but
rather one that is more random. If, however, the underlying ability differences are exerting enough influence in each year, then
some similarities should arise.
The year 2 results for each quartile are shown in the chart below:
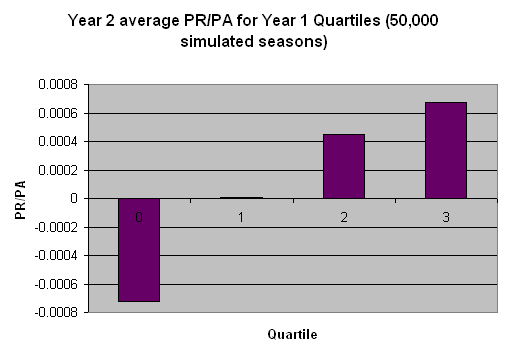
The year 2 chart obviously bears some resemblance to the year 1 chart. Each quartile shows an increase in year 2 PR/PA compared
to the previous quartile. There is definitely some noise–the quartile 1 average isn’t quite as low as the a perfect
distribution would indicate, but the trend is clear.
In the follow-up to the BP99 article that appeared on our Web site in 2000, I limited the set of catchers and pitchers I looked
at to only those pairs of catchers who worked with the same pitcher over a significant number of plate appearances in two
consecutive years. This is very similar to the structure of the simulation, where the difference in underlying ability is
constant. In the real data, both catchers are constant, and if they have a "true" level of ability that doesn’t vary
tremendously from year to year, the difference between them will be relatively consistent from year to year. Note that this
doesn’t mean that the observed differences won’t vary, but rather the true gap between two specific catchers stays about the
same over two seasons.
By doing a similar sort of quartile analysis on the real catcher data (944 sets of data points), we can see if the year 2
average for each quartile looks like the simulated results. As before, I looked at the difference between the two catchers in
years 1 and 2. I divided the year 1 results into quartiles, and looked at the average year 2 difference in PR/PA.
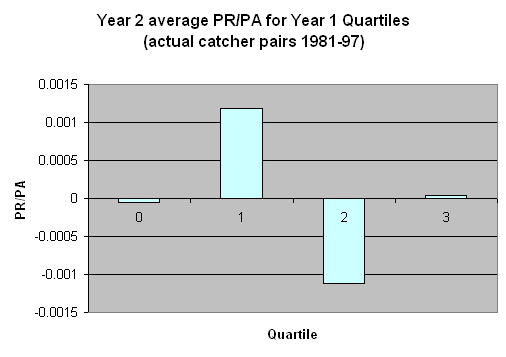
The actual data does not show the pattern we’d expect if there were an underlying catching ability distributed like the
simulations. Rather than a steadily increasing average across quartiles, the middle two quartiles have the most extreme values,
and the direction zigzags as we move across the chart. We’ve simulated what the world would look like if such an ability
existed, and this doesn’t look like it.
It’s possible, however, that the observed difference is due to sample sizes–944 data points versus 50,000. To test this theory,
I selected 1000 data points randomly from the 50,000 sample, and re-ran the analysis.
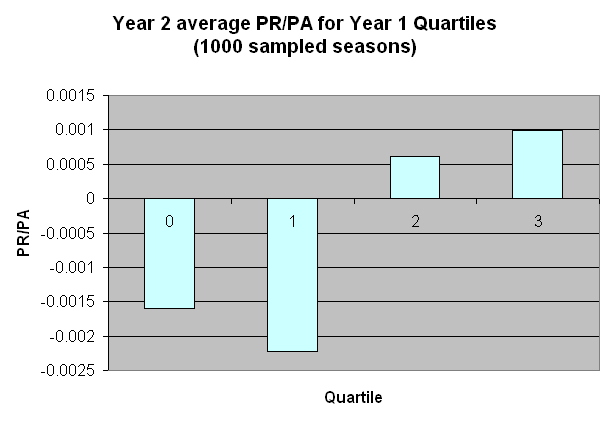
The smaller sample size yielded more deviation from perfection than we saw at 50,000 simulations, but the overall trend of
increasing PR/PA with increasing quartiles is unmistakable. Even at samples similar to what we collected in real life, the shape
of the simulated results differs significantly from the actual results.
So, hearkening back to the James study that helped kick off this article, it is true that a simulated CERA effect can be
difficult to detect, especially if you are looking solely at the ratio of correct predictions of better/worse. However, there
are at least three important things to note:
- First, the demonstration that large amounts of noise that can obscure a real effect exist in yearly catcher measurements
does not prove, conversely, that an effect exists. Instead, it provides an alternate explanation to the null hypothesis, which
is that catchers have no effect on pitcher performance, that is consistent with the data. It neither proves nor disproves either
theory, since both situations would result in data similar to what has been observed.The research presented here does, however, indicate an upper bound on the typical magnitude of an effect, since it becomes more
and more clear as the gap increases. For example, if the typical ability is about +/- 1.00 ERA, there should about a 60/40 split
between two years of data providing matching results versus providing conflicting data. Since we do not see this, we can safely
say that most catchers don’t differ from average by a full run of CERA or more. - Secondly, there are important differences between the model James created, and the one I presented here. The choice of
metric is one. The increased granularity and sample size of PRPA may detect differences that CERA is too coarse a metric to pick
up. The decision to model entire pitching staffs versus isolating pitchers with catcher pairs is another. With the latter
approach, there is less opportunity for other factors to influence the measurements. James does account for this in some parts
of his analysis, however. - The third point is more subtle: there is very little practical difference between saying there is no ability, and that there
is an ability that can’t be reliably detected. Knowing that there’s no way that CERA or similar measures can indicate ability,
and that any other test or scouting report can’t be validated against actual results, means that there’s no actionable knowledge
to be gained.This doesn’t preclude playing a hunch, as some managers are prone to do, but there’s no way to independently establish whether
the hunch was a good gamble or not. The same rational, evidence-based decisions would be made whether an undetectable ability
exists or whether no ability exists. They are, for practical purposes, equivalent, even if they are theoretically distinct. I
acknowledged as much in my original BP99 article:
[…] if there is a true game calling ability, it lies below the threshold of detection. There is no statistical evidence for a
large game-calling ability, but that doesn’t preclude that a small ability exists that influences results on the field.
However, in this case we do not need to suggest that an undetectable ability of this magnitude may exist. The simulated catcher
results where we introduce a range of catcher abilities does yield discernable trends when aggregated into large subsets, rather
than looking at individual data points. Observing the year 2 results from each year 1 quartile of the simulated seasons
indicates that there is a subtle, but detectable difference in how the top year 1 performers do in the versus the bottom year 1
performers. When we look at the actual data from multiple years of major-league play, as was done in my original two articles,
we again find no evidence of a game-calling ability that is consistent with the simulated results.
I want to thank Bill James for the thought-provoking exercise. His original critique and our ensuing e-mail conversations
provided a well-constructed, well-reasoned counterpoint. A simulated approach to modeling catcher’s defense does show that such
an ability is hard to detect using the techniques from my original article, even if we know it’s there, provided it is small
enough (yet still large enough to be of interest). However, a deeper analysis shows that there are still trends that can be
detected in simulated data with a small CERA effect that do not show up in real-life on-field results.
For now, at least, the hypothesis most consistent with the available facts appears to be that catchers do not have a significant
effect on pitcher performance.
Keith Woolner is an author of Baseball Prospectus. You can contact him by
clicking here.
Thank you for reading
This is a free article. If you enjoyed it, consider subscribing to Baseball Prospectus. Subscriptions support ongoing public baseball research and analysis in an increasingly proprietary environment.
Subscribe now