The following article will appear as a chapter in the upcoming book Saving The Pitcher, by BP’s own Will Carroll. To pre-order a copy of Saving The Pitcher from Amazon.com, click here.
To say that Eric Gagne‘s adjective-inducing 2003 performance was just another season would be akin to the notion that the Beatles were just another rock band. The truth of the matter, at least in the case of Gagne, is that his season’s performance was one for the ages. The all-world reliever was not merely good, he was “Nintendo.”
Traditional metrics alone, such as his 55 saves and sporty 1.20 ERA, showed enough to make the goggle-wearing Dodger closer the sexy pick for the National League Cy Young Award, while he further impressed by striking out an astronomical 137 over-matched batters in only 82.3 innings. Further proof that his performance was from another world was his limiting opponents to an eye-popping .133 batting average against.
As is most often the case, the traditional metrics prove to be only the tip of the iceberg in discussing Gagne’s 2003. For all the strikeouts and saves, the bottom line may best be seen through the realization that Gagne was the best reliever in baseball in terms of preventing runs. His 32.6 Adjusted Runs Prevented, based on the analysis of Michael Wolverton at Baseball Prospectus, represents the idea that Gagne prevented approximately 33 runs more than what would have been prevented by the average major league reliever during the course of his specific 82.3 innings pitched. That’s an incredible difference of 3.6 runs for every nine innings pitched.
Similarly impressive, though admittedly less complex, it can be shown that Gagne saved the Dodgers just under 23 runs versus what the team’s starting rotation would have individually allowed had each starter remained in the games they respectively started. This calculation can be done by determining the average number of runs allowed by each individual starting pitcher on the Los Angeles staff, numbers that are also readily available from Wolverton and Baseball Prospectus. As can be seen on the chart, Gagne appeared most often in games started by Hideo Nomo, 16 in total, during which Gagne saved the Dodgers 2.406 runs versus what Nomo would have allowed, on average, in the same number of innings pitched.
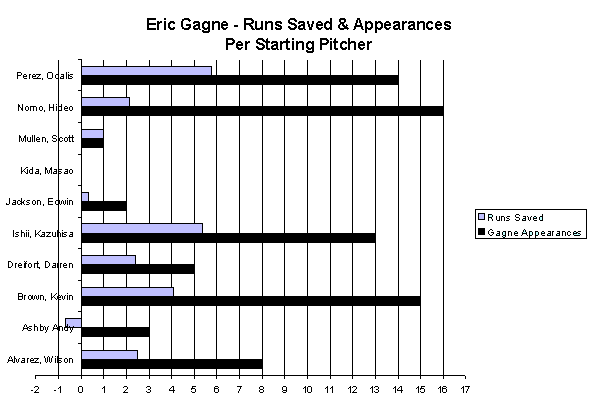
The most aided pitcher on the Dodger staff with regard to Gagne’s efforts was Odalis Perez, who would have given up nearly six more runs in the 14.7 relief innings thrown by Gagne in Perez’s starts. Conversely, Gagne appeared in three of the 12 games started by Andy Ashby in 2003, and can be accused of allowing nearly one run more than what Ashby would have done on his own in those 3.7 innings, the only instance for any of the Los Angeles starters in which Gagne gave up more runs than what the starter would have allowed.
Random Obscenities
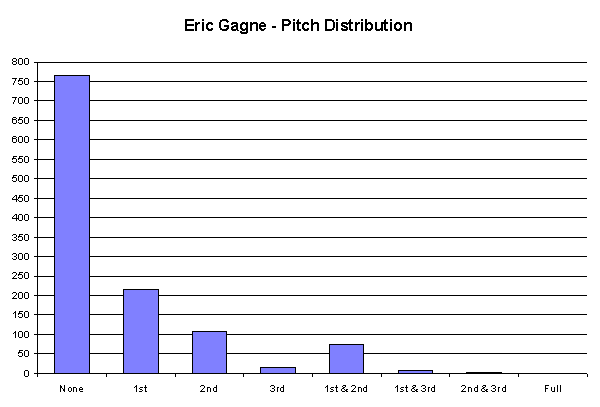
While the prevented run totals quite clearly tell a tale of a phenomenal season, examination of the surgeon-like precision with which Gagne performed should leave no doubt that this wasn’t a fluke. Any pitcher called upon to close the door on 55 wins while only having to throw a single pitch with runners on both second and third base, as was the case with Gagne, cannot be written off as lucky. Especially when one considers the manner in which he was most often used: starting the ninth inning of a save situation. The idea that Gagne not only limited the opposition to a mere 12 runs in 82.3 innings, but that he found himself in the unenviable position of having two runners in scoring position once out of nearly 1200 pitches thrown is simply amazing.
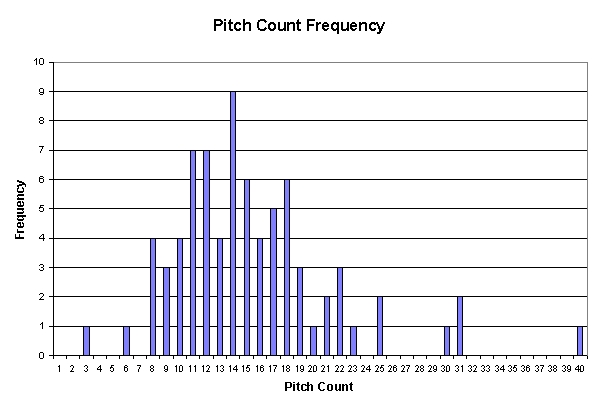
Along with the base situation pitch totals, we can also determine that the median pitch count was 14 pitches (see chart), a number made more impressive by the propensity with which Gagne used the strikeout to retire batters. In needing only 14 pitches to retire an average of just over 3 batters per appearance, the only way one should suspect a high strikeout rate would be through an equally high ratio of strikes thrown. As suspected, Gagne’s ability to throw strikes on 69% of his total pitches thrown went a long way towards making opposing at-bats quick and painless.
A Matter of Perspective
There is no doubt that baseball is indeed a game different than most all others, and this is no more obvious than in examining the central theme of the game itself: the pitcher-batter confrontation. There are few other, if any, instances in all of sport in which the normal manner of competition is that of nine vs. one, such as it is in baseball.
Examining the game in this manner, it can be plainly seen that a large amount of baseball is of a strictly individual matter. Accordingly, and with little surprise, batting statistics are wholly individual in nature. Yet while some batting statistics are simply a means to account for the numerous possible outcomes that can result from a single plate appearance, others attempt to explain the rate at which events occur for an individual batter. All of these statistics, however, are central to the underlying notion that the batter’s only true goal is to put himself in position to score through the avoidance of making outs.
Upon the identification of this goal, the rate at which outs are avoided, otherwise known as on-base percentage, has proven to be an extremely valuable commodity, though quite clearly not the only commodity worth pursuing. The problem is that while a batsman carrying a 1.000 on-base percentage can be said without uncertainty to have perfectly avoided making an out at the plate, the figure alone is not enough to guarantee a subsequent run. The reason, quite simply, is that an individual’s on-base percentage in no way shows whether or not his teammates have, through their own plate appearances, forced the individual into making an out on the basepaths or enabled him to safely cross home plate with a run.
Thus, pitching statistics must be differentiated from simply being an account of the opposition’s batting statistics. Whereas an individual batter’s control is vastly limited once he no longer is the individual being pitched to, the man on the mound is keyed into every at bat of the game. To better illustrate this point, let us examine two separate one inning constructs:
Inning One
Batter A: Base on Balls
Batter B: Ground out, 6-4-3, Double Play
Batter C: Single
Batter D: Fly out
Inning Two
Batter A: Strikeout
Batter B: Strikeout
Batter C: Safe on fielder’s error
Batter D: Fly out
In the above examples it is quite evident to see that using the batter’s metric of on-base percentage the innings were extremely different. Inning One shows the offense to have produced a .500 OBP, whereas Inning Two’s performance produces an .000 OBP. While no manager, executive, or devoted fan would turn their nose up at the prospect of their team maintaining a .500 OBP, it is quite evident that this figure alone is not enough to guarantee runs.
From the pitcher’s point of view, however, both of the above innings were completed in equally efficient manners, as three outs were produced with the pitcher having faced only four batters in both instances. The question is how much credit does the pitcher deserve for the above results? For unlike in the case of the batter, the pitcher is not alone in his dealings. Eight other players play a significant role in assisting the pitcher in their own stated goal: the prevention of runs.
Tom Tippett, in a July 2003 article, produced research in which he suggested the notion that pitchers can in fact have an effect on the batting average of balls put into play. And while batting average is a decidedly batter-centric statistic, the conclusion that can be drawn from the study is that there is correlative evidence suggesting that the pitcher’s abilities have a great deal of impact over the eventual result of individual plate appearances. Whether that be by an individual pitcher increasing the likelihood of a strikeout, decreasing the chances of a walk or home run, or even affecting the overall probability that any ball put into play will result in an out, a pitcher impacts individual plate appearances and should be credited or discredited accordingly.
Thus, where a batter’s ultimate goal is easily broken down into the concept of avoiding outs, pitchers are charged with the responsibility of preventing runs through the creation of outs. The higher the ratio of outs to batters faced, the better a pitcher figures to be in accomplishing his task.
A Dominance Ratio
For pitchers, the concept of perfection within the game of baseball has a rather strict definition. “Perfect” games are reserved only for those select few gentlemen competent enough in their craft to retire every batter faced throughout the course of a single ballgame; 27 up, 27 down. Those able to achieve perfection at the most opportune of times find with it immortality as a rather pleasant by-product. See: Larson, Don.
In a game that presents each at-bat with a limitless array of possibilities, the easiest way a pitcher can guarantee the absolute prevention of opposition runs is to in fact be ‘perfect’. Retiring every batter faced will, without fail, produce a shutout. The reason for this is quite simple: if every batter faced makes an out, there is no scenario possible in which a run can be scored. As such, it should follow that we might be able to gain a reasonable understanding as to the level of a pitcher’s performance by simply determining the proximity a given pitcher comes to achieving “perfection” over a stated time period.
In 40 of his 77 appearances during 2003, Gagne needed only face the minimum number of batters for the amount of innings he pitched. Ignoring for a moment those games in which he entered mid-inning, Gagne assured his team of the complete prevention of runs in what appears to be an amazingly high frequency of just over half of all his appearances.
Interestingly, of these 40.0 innings of supposedly “perfect” relief, one will notice that while Gagne struck out 67 batters, he also managed to give up one base hit. Yes, one base hit. As it turns out, in his August 22, 2003, appearance against the New York Mets, Gagne walked the first batter he faced before a pinch runner was then successfully thrown out attempting to steal second base. Following the caught stealing, Gagne struck out the final two batters of the inning to maintain the perfect batter faced to out recorded ratio.
This, of course, brings to light the intriguing notion that each individual plate appearance needn’t result directly in an out in order for perfect run prevention to be attained; rather, there simply needs to exist an average of exactly three batters faced per inning pitched.
This leaves open the rather absurd opportunity for a pitcher to allow as many as 18 hits over a nine-inning span while still maintaining a three-to-one ratio. That is, of course, provided the innings are sequenced in such a manner that two base hits open the inning while the third batter promptly hits into a triple play. For in this example, the perfect batters faced to inning pitched ratio still stands. The odds such an occurrence happening in a game are admittedly slim, though still possible.
In considering the ratio of batters faced to innings pitched, one might see similarities with that of Craig Wright’s ground-breaking concept of Batters Faced per Start (BFS). Whereas BFS can be used to evaluate pitcher workload with an eye towards forecasting performance dropoffs and even injuries, the use of batters faced to innings pitched can be seen as a form of a dominance ratio applicable to starters and relievers alike.
What such a dominance ratio does not do, however, is depict the proximity of a pitcher’s performance to that of a “perfect” performance in a way that is easily comparable to other pitchers.
In again considering Gagne’s 2003, we can rather readily see that in 82.3 IP, he faced a total of 306 batters. Had Gagne faced only the minimum, he would have needed to face only 247 batters to complete 82.3 innings pitched. Thus, Gagne was 59 batters over the ‘perfect’ value.
A rather quick evaluation shows that those extra 59 batters Gagne faced account for roughly 24% more than had he pitched ‘perfectly’ throughout the 2003 season. To then nominalize this value with respect to the notion that, much like in grade school, 100% is a perfect score, Gagne can be pegged as having achieved approximately 76% of total ‘perfection’ in 2003.
While a free-standing figure of 76% has very little value outside of a well stated context, perusal of data for the past 10 major league seasons provides a suitable starting point. Between the first pitch of 1994 and the final out of the 2003 season, a total of 22,708 regular season games were played at the major league level. In those games, over 1.76 million plate appearances occurred in exactly 405,394.0 innings pitched.
Dominance Perfection Games
Season IP PA Ratio Percentage Played
1994 28,586.3 124,483 4.355 54.85% 1,599
1995 36,032.0 156,703 4.379 55.03% 2,016
1996 40,560.7 177,261 4.370 54.32% 2,266
1997 40,454.0 175,541 4.339 55.36% 2,266
1998 43,415.0 188,191 4.335 55.51% 2,430
1999 43,211.3 189,518 4.386 53.81% 2,421
2000 43,244.3 190,261 4.400 53.34% 2,428
2001 43,287.3 186,976 4.319 56.02% 2,428
2002 43,269.0 186,615 4.313 56.24% 2,425
2003 43,335.3 187,448 4.326 55.82% 2,429
Total 405,395.3 1,762,997 4.349 55.04% 22,708
By then calculating the corresponding dominance ratio, and nominalizing it to the same scale as Gagne’s figure of 76% in 2003, we see that the corresponding percentage for all Major League pitchers over the past 10 seasons is approximately 55%. Further, in looking at the individual totals for each of the ten seasons, the range can be easily identified as between 56.24% in 2002, and 53.34% in 2000.
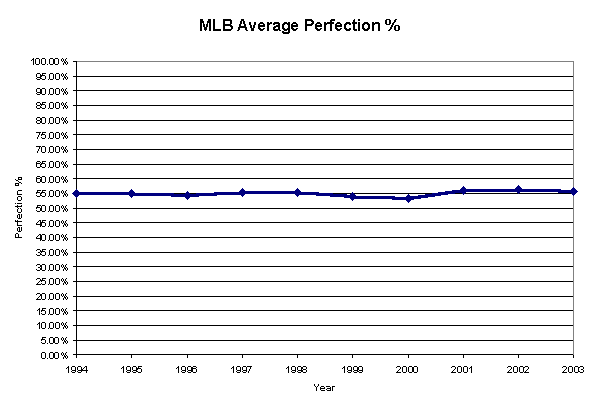
Inferable from these figures is the notion that the average Major League Baseball game over the past 10 seasons can be said to have been pitched at a level only slightly more than half way to the level of perfection. Appropriate, when one considers the fact that pitching a perfect game is among the most difficult accomplishments in the game.
Further, in maintaining a constant value of innings pitched, a linear relationship can be seen to exist between batters faced and the resultant percentage.
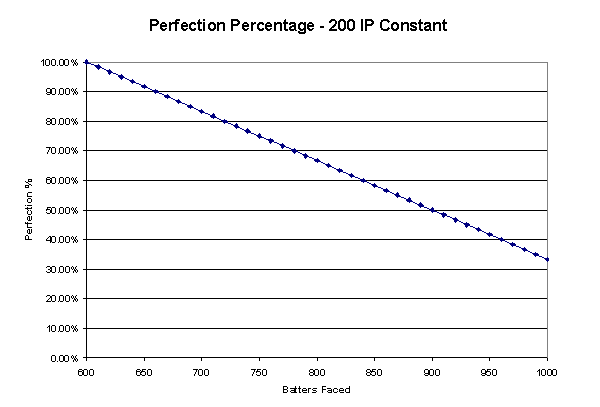
Thus, we introduce…
Perfection Percentage
Defined through the equation below, Perfection Percentage allows us to quickly and rather easily determine exactly how close to perfect a pitcher can be said to have performed over a given period of time.
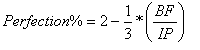
Perfection Percentage is bound by a maximum value of 100% at one end of the spectrum, while a performance reminiscent of David West, circa October 1991, muddies the other end of the scale with a dreaded “divide by zero” phenomenon. In the case of all pitchers able to record at least one out, a negative value becomes possible once the dominance ratio of BF to IP exceeds that of a 6-to-1 ratio.
One quite evident hindrance is that Perfection Percentage does not take into account, nor make adjustments for, the help and/or harm done by fielders with respect to double plays turned or errors committed. What Perfection Percentage quite clearly does measure, however, is the efficiency with which pitchers create outs.
How Can We Use It?
The first hurdle faced by Perfection Percentage is that of the question posed by: How is it better than a simple measure such as Earned Run Average?
In order to answer this, we must first consider the idea presented by the book, The Hidden Game of Baseball, by John Thorn and Pete Palmer. The Hidden Game of Baseball presents a table with which a person can easily look up the probable number of runs that would be scored for a given bases and outs scenario. Intuitively, Thorn and Palmer’s table suggests that the probable number of runs scored following a leadoff triple is greater than that of the probable runs following a two-out, bases empty, walk. These probabilities are based upon years of game data, which is a vastly greater sample size than that of an individual starting pitcher’s theoretical 200 innings pitched in any given season.
Yet while each of the 200 innings pitched by a real-life starting pitcher are affected by the rules of probability, there clearly exists a randomness with respect to when exactly a runner with a 20% chance of scoring will actually do so in a one-inning, real life example. Therefore, a seasonal ERA total, through this built in randomness, can be quite different between two pitchers of extremely similar peripheral numbers.
Perfection Percentage, meanwhile, is not concerned with the actual number of runs scored against a given pitcher, but instead the degree to which a pitcher leaves himself open to the probability of runs scored. In this way, Perfection Percentage gives us the luxury of being primarily concerned with an area in which a pitcher has a far more solid ability to control, that of limiting baserunners through the efficient creation of outs, and less with the end result of a comparatively arbitrary runs allowed total.
No Hitters
One of the consequences of dealing only in terms of batters faced and innings pitched is that walks, hits, errors, and hit batsmen all essentially count the same. A concept that may come as some sort of consolation to Kevin Orie when evaluating Kerry Wood‘s performance on May 6, 1998.
In comparison to the nine-walk, one-beanball, no-hit performance of Marlin A.J. Burnett on May 12, 2001, Wood’s 1998 gem grades out far better by a margin of 92.59% to Burnett’s 62.96%. This, despite the obvious fact that Burnett’s performance was well celebrated for being of the no-hit variety, while Wood allowed only two baserunners, a hit batter and an, at the time questionable, base hit. Though one mustn’t look beyond Andy Hawkins to realize that even all no-hitters are not created equally, there is another reason why Wood’s game is considered a possible selection for the title of ‘Greatest Game Ever Pitched’ while Burnett’s is not; 20 strikeouts.
In highlighting another interesting aspect of Perfection Percentage, we note that Kerry Wood’s record-setting outing would have been unchanged in the eyes of Perfection Percentage had he struck out 2, 10, or even 27 batters. Making it important to realize that Perfection Percentage can be an incredibly useful tool, but it is by no means the Swiss Army’s long-awaited entry into the field of baseball statistics.
Today’s Players
Examination of a handful of current major league pitchers shows that rankings based solely on Perfection Percentage appear to be relatively in line with the what the common consensus of who the top pitchers in the game currently are. The one obvious distinction is that today’s closers exhibit career marks, as a whole, better than even those of the top tier of starting pitchers. A point that seems logical when considering the differences that exist between the two roles. Closers are expected to work efficiently for little more than a single inning at a time, and if they do not perform to a specified level, they will not be long for the job. Additionally, in many cases with closers, a big inning has the potential to end prematurely with either a blown save and a loss, or a change of pitcher. In both instances, however, the batters faced totals by a closer would appear less than that of a premier starting pitcher asked to pitch out of a mid-game jam in order to continue eating innings.
One might also have a rather Darwinian expectation that any major league pitcher boasting more than a cup of coffee in the show would have to perform at a minimal level of success. As such, simply attaining a Perfection Percentage of the league average for an extended period of time is nothing to slouch at, instead it only makes further impressive the efforts of those players above league average.
The Left-handed Odd Couple
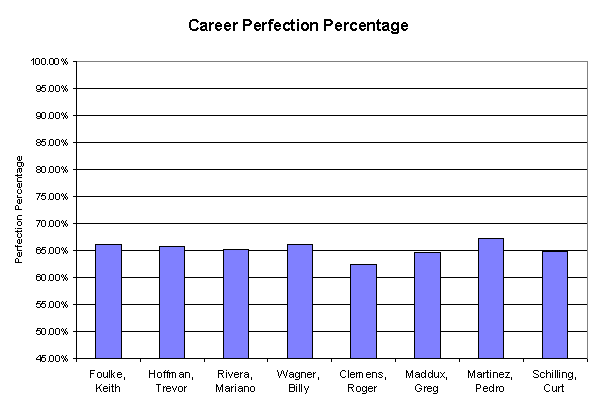
Randy Johnson did not truly become a Cy Young-caliber pitcher until well into his career, something that can clearly be seen through the season by season chart of his career’s Perfection Percentages. Prior to 1993, Johnson led the league in walks three consecutive years in a row, averaging over six walks per game in both 1991 and 1992. In 1993, however, Johnson curtailed his control problems and went on to a career perfection percentage of 65.59% over the next 10 seasons, doing so with a great deal of consistency helped by his 12.03 strikeouts per nine inning rate.
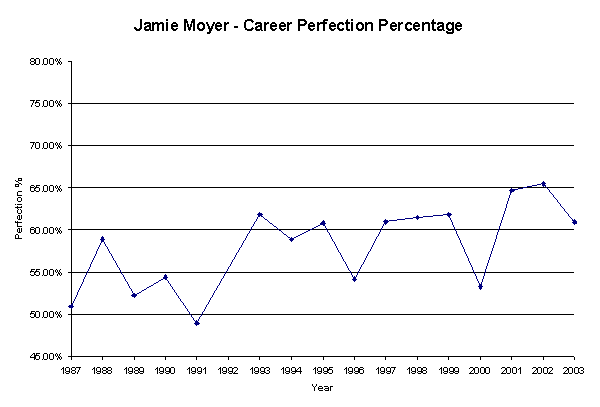
Meanwhile, Jamie Moyer has been credited rather appropriately in the later stages of his career with a masterful ability to limit the batting average of balls in play of his opponents. Corresponding to this newfound ability, Moyer’s Perfection Percentage has changed rather dramatically over the past several seasons as well with a 63.73% mark from 2001 through 2003.
A Rhodes Less Traveled
Fans of reliever Arthur Rhodes may be quick to point out that the lefthander’s 2002 Perfection Percentage figure of 77.03% was actually higher than that of Gagne’s 76.11% in 2003. This brings forward the idea of combining Perfection Percentage with strikeout rates for a more complete overall evaluation, because strikeout rates become important in understanding the repeatability of a pitcher’s level of dominance.
Take for example the following two pitchers:
IP BF SO Pitcher A 100 300 50 Pitcher B 100 300 200
Quite clearly, strikeouts produce a noticeably intuitive difference between two otherwise equal pitchers, both of whom produced a perfect efficiency in creating outs. Pitcher B appears more dominant overall, and more probable to maintain such a level of perfect dominance. For even though pitchers have been shown to have a degree of control over the batting average of balls put into play, outs produced in this manner are not nearly as guaranteed as a strikeout. Thus, Pitcher A leaves himself more open to the possibility of baserunners being created by bad hops eating up infielders, etc.
To this degree, in having two pitchers of nearly equal Perfection Percentage, as is the case between Gagne and Rhodes, the pitcher with a higher strikeout rate should in most instances have a better chance of repeating an established level of Perfection Percentage.
In taking nothing away from a season in which Rhodes exceeded the out creation efficiency of the average of his peers by 22%, his well above average strikeout rate of 10.46 per nine innings still falls shy of Gagne’s 14.98 strikeouts per nine innings in 2003. Based on this, Gagne could be given an ever so slight edge in being able to repeat his results if having to essentially do the season over again. Though, clearly, Rhodes would not be expected to fall back to the performance of a merely league average pitcher.
One More Gagne
Being that the original thoughts regarding the creation of a Perfection Percentage came directly from close examination of his season’s game logs, I thought it best to end up there as well.
Having already discussed Gagne’s median pitch count of 14, we can now gather a quick overview of his effective efficiency based on the actual number of pitches thrown in each appearance. Noting the chart, it should come as a shock to no one that when throwing less than the median number of pitches, Gagne’s already sky-high Perfection Percentage begins to take orbit. In 29.3 innings over 31 appearances in which Gagne threw 13 pitches or less, his overall Perfection Percentage was a staggering 88.51%. In 11 appearances when throwing between eight and 10 pitches, he needed a total of a mere 99 pitches to record 11.0 innings against 34 batters, representing a Perfection Percentage of 96.97% and an average of 2.91 pitches per batter faced.
Pitches/Appearance G IP BF Pitches K Perfection % Below Median 31 29.0 97 321 46 88.51% Median 9 8.7 33 126 15 73.08% Above Median 37 44.7 176 737 76 68.66% Total 77 82.3 306 1184 137 76.11%
Likewise, when stretched beyond the 14 pitch count median, Gagne’s Perfection Percentage drops to a figure of 68.66%, which is still 13% above the league average pitcher. In those 37 appearances and 44.7 innings pitched, Gagne threw a total of 737 pitches to 176 batters, an average of 4.19 pitches per batter faced.
In noting the pattern that a lower pitch per batter faced ratio represented a higher Perfection Percentage, it must be noted that the sample size of one player’s season is not nearly enough to run blindly off the cliff of correlation like lemmings in search of some sort of Perfect Pitch Count Percentage. Having said that, however, further investigation of such a phenomenon could prove to be immensely valuable in breaking down the numerous pitching philosophies’ respective approaches to setting up hitters.
All of which brings us to a truly ponderable question: Can an individual pitch be perfect? Or can it merely be appropriate?
Either way, the most notable impact of Gagne’s remarkable relationship between pitches per batter faced and Perfection Percentage is the understanding that when he was ‘on’, opposing batters would have been no less effective swinging a nine-iron wildly around the batters’ box. It is this, more than any other aspect of his game log, that is the single most damning bit of evidence against Gagne in any ill-advised arbitration hearing between the pitcher and his employer; he was far too quick to finish innings. Gagne faced only three batters in one-inning appearances an amazing 34 times in 77 appearances. By the time fans worked up the energy to scribble “G-A-G-N-E” onto their scorecards, the game was already over.
Blake Kirkman was the research assistant for the upcoming book Saving The Pitcher, by Will Carroll. This piece will be a chapter. Blake is currently employed by an MLB team, working in media relations. He can be reached at bkirk79@yahoo.com.
Thank you for reading
This is a free article. If you enjoyed it, consider subscribing to Baseball Prospectus. Subscriptions support ongoing public baseball research and analysis in an increasingly proprietary environment.
Subscribe now