Baseball ProGUESTus: Jeff Clement, Mike Morse, and the Value of Making Mistakes

Believe it or not, most of our writers didn't enter the world sporting an @baseballprospectus.com address; with a few exceptions, they started out somewhere else. In an effort to up your reading pleasure while tipping our caps to some of the most illuminating work being done elsewhere on the internet, we'll be yielding the stage once a week to the best and brightest baseball writers, researchers and thinkers from outside of the BP umbrella. If you'd like to nominate a guest contributor (including yourself), please drop us a line.

​Graham MacAree is the Lead Soccer Editor at SB Nation. He co-founded Statcorner and invented tRA. He also owns multiple Jeff Clement jerseys.
 

In retrospect, it seems fairly silly. But when the ball left Jeff Clement's bat on September 28th, 2007, I knew I was watching the next good, homegrown Seattle Mariners hitter. Everything I knew told me he was going to succeed. A .275/.370/.497 line at Triple-A Tacoma in his age-23 season satisfied my statistical cravings. His swing looked good, his plate discipline superior. Sure, his defense was atrocious, but I thought catcher defense didn't really matter. Scratch that: I knew it didn't matter.

Like I said, it does seem rather silly now. After 397 major-league plate appearances, Jeff Clement is the proud owner of a .664 OPS. And he doesn't even catch anymore. Everything I thought to be true about Clement (apart from his rugged handsomeness) turns out to have been entirely wrong.

While I was drooling over a Clement-filled future in Seattle, Mike Morse was having a similar year. He hit a little worse in Tacoma and a little better in Seattle as a 25-year-old. He was, however, clearly terrible in the field, no matter where you stuck him—a few months later, he'd injure himself trying to make a play in the outfield—and he had nothing like Clement's reputation or track record as an elite hitting prospect. When Morse was dealt to the Washington Nationals for Ryan Langerhans, I'm reasonably sure I let out an audible “Whoop.”

That seems pretty silly in retrospect as well.

It's extremely tempting to chalk up my many errors in player valuation to bad luck. Anyone with a serious interest in the game is fully aware that it's almost impossible to accurately project how players will do in the future. Getting things wrong isn't just acceptable, it's expected. We don't have perfect models for player aging, and even if we did, our inability to measure player talent accurately at any given moment would add a huge element of unpredictability to our projections.

So, given the huge barriers that the universe has put in place to prevent us from ever getting remotely close to accurately analyzing baseball players, we expect to be wrong rather a lot. And that’s completely fine. Nobody’s expecting us to be right 100 percent of the time, or anywhere close. But at the same time, that does give us something of a crutch when things go wrong, because it’s very easy to assume that the random element rather than the process is responsible.
 
Paul DePodesta is very fond of the two-by-two process versus outcome matrix. For those unfamiliar with it, it’s a pithy way of describing scenarios regarding how things play out against how they were expected to:

As DePodesta wrote:

We all want to be in the upper left box – deserved success resulting from a good process. This is generally where the casino lives… The box in the upper right, however, is the tough reality we all face in industries that are dominated by uncertainty. A good process can lead to a bad outcome in the real world. In fact, it happens all the time. This is what happened to the casino when a player hit on 17 and won.

This is all true, of course. The problem, however, is that we don’t really know what good process is. We might think we know, but the only way to test that out is to play out our supposed good processes and see what the results look like. There’s an uncertainty in terms of our perception of process on top of the random variance we all know about. That puts us in an interesting situation vis-à-vis the top right and bottom left corners.

If you ignore the fact that we’re not entirely sure we know what we’re doing, this is what your process/results table ends up looking like:

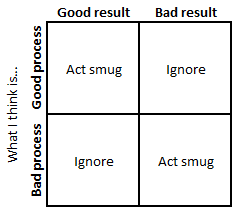
I think everyone reading this has seen something like that matrix before. I’ve certainly indulged in some combination of being smug about being “right” and ignoring being “wrong” in my time. It is far too easy, at least when you’re looking at something like baseball, to assume that when your model gives wrong results, it’s actually the universe that’s in the wrong. If the Boston Red Sox are terrible, that’s just the result of luck over a small sample. But boy, we sure were right about the Rangers being amazing!

The way our brains process statistics appears to be significantly different from the classical versions of the mathematical discipline. Instead of relying on significance levels and sample sizes, they seem to approach the world in a way similar to what’s known as Bayesian inference, which was developed formally in the 1800s by Pierre-Simon Laplace.

I’m not going to go into a great deal of detail here—I’ll leave that to the real statisticians rather than the engineer-cum-sports-bloggers, especially because I have no intention of doing any real mathematics—but the general gist of it is as follows: new information incrementally updates your previous knowledge by some amount. Sounds simple enough, right?

We all approach baseball with some set of prior beliefs. This is why it’s more interesting, say, when Madison Bumgarner hits a home run than when Joey Votto does it. Seeing Votto hit 13 dingers in 300-odd at-bats doesn’t change my opinion of him at all; seeing Bumgarner homer in any number of them makes me realize that he’s actually physically capable of doing so, which is especially jarring because prior to that home run I simply assumed he was not.

That’s a trivial example, of course, but the point of this little diversion into quasi-statsland was to show that small events (there have, after all, been lots of home runs hit this year) can have significant changes on a world view. Previously, I had lived in a universe where Madison Bumgarner did not hit home runs; now I live in one where he does.

Looking back a little further, we can apply a similar approach to our models. Every single time something pans out as projected, we can be more confident that what we’ve done is correct. Every time it doesn’t, we should be a little less secure in our belief that we’re right.

Ultimately, it’s being wrong that’s inherently more valuable. Right now, we operate in a world where most analysis is limited and known to be limited. Areas in which we’re regularly wrong simply denote regions ripe for improvement. We cannot learn anything by being right, and there’s still clearly plenty left to learn.

So instead of worrying about being wrong, it would be nice if baseball analysts continued to own their mistakes, figuring out what happened, why it happened and how to make sure it stops happening. As the industry matures and takes itself more seriously, there seems to be less willingness to do so. That’s unfortunate.

Unless we’re systematically wrong about a lot of things, baseball analysis (and a lot of other far less important disciplines) will never progress. Many clever people getting things wrong, acknowledging those mistakes, and then learning from them—focused wrongness, if you like—is the path by which genuine improvement can be made.

After all, the next great pitching stat will be wrong. Defensive statistics? Wrong again. Aging curves? All wrong. I’m reasonably sure that everything sabermetrics knows about baseball is wrong to some degree. But that’s why it’s still interesting. Finding out where we’re wrong and fixing those issues is, or should be, the main thrust of baseball research.

And even when you don’t know why you were wrong (e.g. Jeff Clement flopping, Mike Morse hitting)—it’s always good to be a little less confident in our own abilities. A bit of humility never hurt, right?